Violation of classical inequalities by frequency filtering
Photon correlations are a resource for quantum information processing. If only for the particular case of quantum cryptography: at the single photon level, they can be used for the BB84 protocol. At the two-photon level, they can power the Ekert version[1] that relies on entanglement. It is one requisite if we are to develop a quantum technology to find, engineer and optimize photon correlations.
We have shown in a series of papers[2][3][4] how one can use the frequency of the photons emitted by a quantum source as an added useful degree of freedom for quantum correlations. In our last input into this theme, now available on the arXiv[5], we study how frequency filtering impacts on the violation of classical inequalities, namely, on the Cauchy-Schwarz inequality (CSI) and a brand of Bell's inequality (BI). These are the most standard and, surely, also the most important relationships to ensure that, when violated, one is in presence of a genuine quantum behaviour.[6]
What we did in our paper "Violations of classical inequalities by frequency filtering" by Carlos Sanchez et al., is to show that one can put these inequalities to the test not only for the modes of some Hamiltonian representation, as is usually done theoretically, but more directly for the photons emitted by these modes. This can be an important difference because photons are indistinguishable and can interfere in a way that is not accounted for if you look at mode correlations.
Let us consider an example. Say you have a mode $\color{blue}{\sigma_1}$ that emits blue photons and another mode $\color{red}{\sigma_2}$ that emits red photons. This is the situation sketched in the upper part of the picture below.
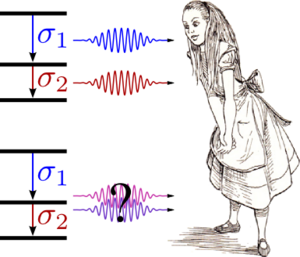
Alice considering whether the photons emitted by two modes $\color{blue}{\sigma_1}$ and $\color{red}{\sigma_2}$ behave classically or not. In a simplified picture, she considers that the photon correlations are identical to the underlying modes correlations. In the real world, however, photons cannot be unambiguously attached to the modes that emitted them, and as a result, the photon correlations that are observed do not correspond to those computed from the modes. An exact theory of detected-photon correlations is needed for that purpose. (Alice's graphics art by (or for) Robert Gilmore).
Already we have presented the problem in terms of coloured photons. Indeed, violations of CSI and BI are often performed with the frequency degree of freedom (polarization is another classic).
Now the photon statistics of these modes being defined as:
\begin{equation} \tag{1} g^{(2)}_{ij}=\langle \sigma_i^\dagger \sigma_j^\dagger\sigma_j\sigma_i \rangle/(\langle\sigma_j^\dagger\sigma_j \rangle \langle\sigma_i^\dagger\sigma_i \rangle)\,, \end{equation}
for $i,j=1,2$. The CSI would then be challenged by checking whether:
\begin{equation} \tag{2} \left[g^{(2)}_{12}\right]^2\leq g_{11}^{(2)} g_{22}^{(2)} \end{equation}
is true, in which case the classical inequality is obeyed and the observation is compatible with a classical world. If, on the other hand, $[g^{(2)}_{12}]^2>g_{11}^{(2)}g_{22}^{(2)}$, mode-to-mode correlations overcome the mode autocorrelations in a way that is unaccountable by a classical description. It violates that inequality that brings us, among other things, the triangle inequality: $\|x+y\|\le\|x\|+\|y\|$.
Now, the experimentalist—that would be Alice in the image above—does not actually look at the mode correlations per se, but at the photon correlations from the photons emitted by these modes. This would be essentially the same thing for most practical purposes, and in fact is even exactly so for single-photon observables, but for photon correlations, it turns out that the mode correlations can be either too restrictive, wrong or both.
There are various shortcomings but one will be enough to illustrate the idea. When Alice detects photons, she would probably assume that blue photons come from the blue mode and red photons from the red mode, and this is indeed the case for most photons. But sometimes, because things fluctuate, the blue mode will emit a red photon, and vice-versa. In which case, the mode correlation and the detected coloured-photon correlation would differ. When the photons are difficult to distinguish in the first place, say because the modes overlap a lot, this can become a source of large errors.
And there is an issue here, because:
- Mode correlations is what the theorist computes.
- Photon correlations is what the experimentalist measures.
What we did in the manuscript is to compute photon correlations.
By doing so, we have also been able to compute all photon correlations, not only those defined by the underlying mode in the theoretical description, but, say, photons from opposite tails of a spectrum. This is something you cannot do in a mode-correlations theory, because the mode is identified with the peak itself (its lineshape is essentially ruled by its lifetime and its coupling to other modes). Now, this is crucial because the stronger correlations are precisely not those from photons that one would attach to the modes, but are offset in the spectrum.
We found various interesting results, but again I will comment on only a few of them. We have considered a particular emitter, known as resonance fluorescence (the spectral shape itself is called the Mollow triplet), but these results are general.
One clear result is that we have been able indeed to provide a full mapping of photon correlations and show the landscape of violation of CSI and BI, uncovering surprisingly rich and different structures, in particular for the Bell's inequalities. You can see in a YouTube video[7] how these landscapes evolve as a function of the frequency window you ascribe yourself to define your photons (alternatively, that would be the bandwidth of filters with which you select photons before measuring their correlations). In the video, you see the CSI violation in green in the middle panel and the BI violation in red in the right panel (left panel is the Glauber's correlation functions, that is discussed elsewhere). Such results show that a comprehensive description of photon correlations, taking into account conjugate variables such as frequency and time (zero-delay for the published results), are tractable, at least theoretically (which has now the upper hand again; correlating regions of the spectra with little emission is experimentally more challenging, but surely the main difficulty was to know one had to look there in the first place).
Another major result is the one already mentioned, that violations are maximum not where they are expected to be, namely, from transitions between excited states of the system. The reason is that strongly correlated photons are those which arise from a transition that involves a virtual state, and these usually are shot at different energies than are defined by the modes. As a conclusion, instead of correlating peaks, one should detect photons from unlikely frequencies of the spectra, such as in the tails, or in-between the peaks. Again, this is a computation that the usual mode correlation approach cannot reach. By looking at photons from the elbows of the spectral shape, for instance, the BI can be made to approach its theoretical maximum of $2\sqrt{2}$.
Thus, since photon correlations are a resource for quantum information processing, it is important to be able to optimize them. Our theory shows how to do so. From there on, one can envision how to go the next step and design actual quantum devices taking advantage of such boosting of the correlations from spectral filtering. This is work in progress.
References
- ↑ Quantum cryptography based on Bell's theorem. A. K. Ekert in Phys. Rev. Lett. 67:661 (1991).
- ↑ Theory of Frequency-Filtered and Time-Resolved $N$-Photon Correlations. E. del Valle, A. González-Tudela, F. P. Laussy, C. Tejedor and M. J. Hartmann in Phys. Rev. Lett. 109:183601 (2012).
- ↑ Distilling one, two and entangled pairs of photons from a quantum dot with cavity QED effects and spectral filtering. E. del Valle in New J. Phys. 15:025019 (2013).
- ↑ Two-photon spectra of quantum emitters. A. González-Tudela, F. P. Laussy, C. Tejedor, M. J Hartmann and E. del Valle in New J. Phys. 15:033036 (2013).
- ↑ Violation of classical inequalities by frequency filtering, C. Sánchez Muñoz, E. del Valle, C. Tejedor and F. P. Laussy, arXiv:1403.6182 (2014).
- ↑ Violations of classical inequalities in quantum optics. M. D. Reid and D. F. Walls in Phys. Rev. A 34:1260 (1986).
- ↑ Violation of Cauchy-Schwarz and Bell's inequalities in resonance fluorescence at https://www.youtube.com/watch?v=2LvUA4jDvIU.