Wading through the Hilbert space

Revision as of 11:20, 29 May 2017

The Hilbert space is a big place. In the words of Douglas Adams (?!):

Bigger than the biggest thing ever and then some. Much bigger than that in fact, really amazingly immense, a totally stunning size, real 'wow, that's big', time. Infinity is just so big that by comparison, bigness itself looks really titchy. Gigantic multiplied by colossal multiplied by staggeringly huge is the sort of concept we're trying to get across here.

We think we know it well because its canonical basis makes it look easy. Every member of the space comes in the form:

$$\sum_{k=0}^{\infty} \alpha_k\ket{k}$$

Really easy. The $\alpha_k$ are complex and they have to be normalized, $\sum_{k=0}^\infty|\alpha_k|^2=1$, but this is just basic linear algebra stuff.

That is actually deceiving as we're not quite gifted in imagining all the structure that may arise from an infinite set of complex numbers. When we think of quantum states, we think in terms of families. The simplest one are those that constitute the canonical basis, the Fock states $\ket{k}$. That's one photon for you: $\ket{1}$.

Then, since Glauber, we know of coherent states $\ket{\alpha}$, Poissonian superpositions of photons, and thermal (also called "chaotic") states, with exponentially decaying probabilities from vacuum. Thermal states are also statistical mixtures but that doesn't matter too much. Oh, and I forgot vacuum $\ket{0}$ although we mentioned it already. That's already quite of a good collection. I'm sure I wasn't the first but in 2006 I introduced mixtures of thermal and coherent, that I called, rather loosely, "cothermal states" Effects of Bose-Einstein condensation of exciton polaritons in microcavities on the polarization of emitted light. F. P. Laussy, I. A. Shelykh, G. Malpuech and A. Kavokin in Phys. Rev. B 73:035315 (2006). . You can also interpolate between Fock and coherent states Glauber--Sudarshan P representation of negative binomial states. K. Matsuo in Phys. Rev. A 41:519 (1990).. I don't know of interpolations between Fock and thermal states but this is certainly not difficult to work out. There is also the big family of squeezed and Gaussian states.

Still, all these states are far from providing even a small portion of what populates the whole Hilbert space, even though they are the most important instances.

Why would you care? Beside curiosity, a first reason came from our exciting with quantum light line of research. When you excite something with any of the funny new sources that we develop, you typically bring your target in a quantum state that is not a member of the family above (showing again how it fails to be comprehensive; our first exploration already brought us away from the lobby of the Hilbert hotel).

Take the simplest source, the single photon source (SPS). How does a quantum harmonic oscillator swing when you drive it with a SPS? It's not a Fock state $\ket{1}$. What is it? (it's easy, compute it). But more than that, what could it be? What states can we drive with a SPS? What states can we drive with any source at all? What states are in fact possible?

With Eduardo Zubizarreta Casalengua, a Master student in our group, we worked out in detail a new charting of the Hilbert space, that we had introduced earlier Excitation with quantum light. I. Exciting a harmonic oscillator. J. C. López Carreño and F.P. Laussy in Phys. Rev. A 94:063825 (2016). . The rulers are the Glauber correlators, $n_0$ (the mean population) and $g^{(n)}$, the $n$th order coherence function:

$$g^{(n)}\equiv\langle a^{\dagger n}a^n\rangle/\langle\ud{a}a\rangle^n\,,$$

where $a$ is the annihilation (ladder) operator.

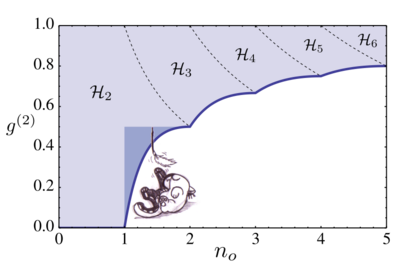
This is how the Hilbert space for up to 3 particles (we call it $\mathcal{H}_3$) looks like:

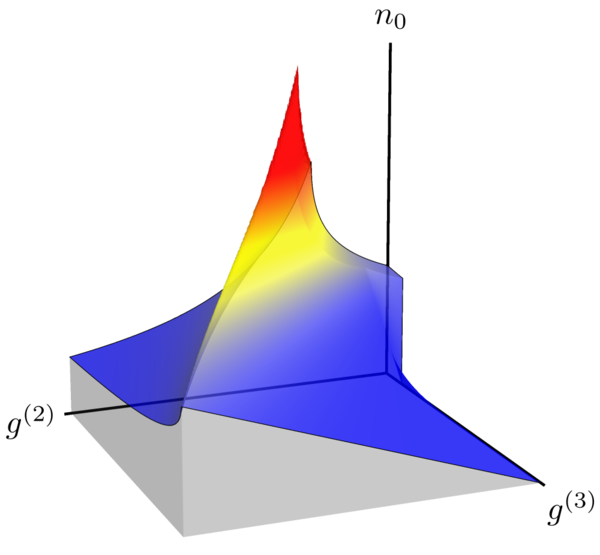
Since we have three particles at most, $g^{(4)}$ and all higher $g^{(n)}$ are zero. What this shows is the boundary for the allowed physical states (that exist for a given $(n_0, g^{(2)}, g^{(3)})$. Everything above this circumvoluted surface is forbidden, everything below till the floor (set by $n_0=0$) is allowed. Beyond the boundary, we have also worked out the density of states $\mathcal{P}_g \left( n_0, g^{(2)},g^{(3)}\right)$ populating this charting of the Hilbert space, which is shown on the surface by the colour (which could also be extended to the space below, which we don't do for clarity).

The expression for the density of probability is remarkably simple (you can find it in the text, Eq. (25)) and depends only on the population... but it is defined in a complex geometrical space. Considering projections allows to get a better grip of how the states are distributed:

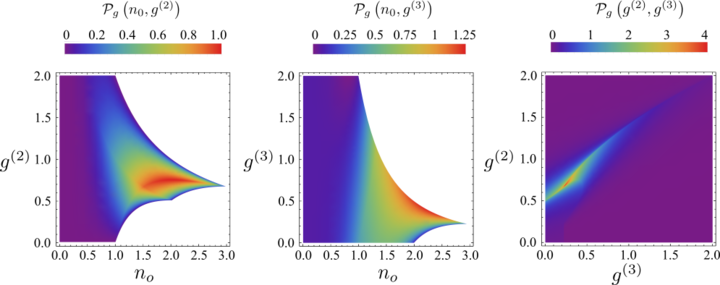
If you pick up a state randomly that has at most 3 particles, these are the chances that you will find it with such and such a population and particle fluctuations. Importantly, there are some limits to the allowed values you will get. Namely, your state has to satisfy:

$$\max\left( n_0 \g{3},\frac{n_0 \g{3}}{3}+\frac{2}{n_0}-\frac{2}{n_0^2}\right) \leq g^{(2)}\leq\frac{n_0\g{3}}{2} + \frac{1}{n_0}\,,$$

and

$$ \max\left(0,\frac{2 g^{(2)}}{n_0}-\frac{2}{n_0^2}\right)\leq g^{(3)}\leq\min\left(\frac{g^{(2)}}{n_0},\frac{3 g^{(2)}}{n_0}-\frac{6}{n_0^2}+\frac{6}{n_0^3} \right)\,,$$

Eduardo Zubizarreta Casalengua

One can obtain the probabilities for the oscillator to have $i$ excitations from the knowledge of all the $g^{(j)}$. In the space of up to $N$ particles:

$$P_i= \sum_{j \geq i}^N (-1)^{i+j} \frac{g^{(j)}n_0^j}{i! (j-i)!}\,,$$

In the space of up to 3 particles, with states $\alpha_0\ket{0}+\alpha_1\ket{1}+\alpha_2\ket{2}+\alpha_3\ket{3}$, the density of probabilities reads:

$$\mathcal{P}_g (n_0, g^{(2)}, g^{(3)}) = \frac{n_0^5}{2} \Theta \left(\mathcal{g}_3\right)\,,$$

The general case reads:

$$\mathcal{P}_g \left( n_0, g^{(2)},\ldots,g^{(N)} \right) = \frac{n_0^{(N^2+N-2)/2}}{\mathrm{sf}(N-1)} \Theta({\mathcal{g}_N})\,,$$

The boundaries are:

$$\frac{2}{n_0}\geq g^{(2)} &\geq \frac{\lfloor n_0 \rfloor (2n_0 - \lfloor n_0 \rfloor -1)}{n_0^2}\,,$$

and many have waded through

This is from Quantum correlation among photons from a single quantum dot at room temperature. P. Michler, A. İmamoğlu, M. D. Mason, P. J. Carson, G. F. Strouse and S. K. Buratto in Nature 406:968 (2000).: (here technically they don't refer to the 1/2)

This is from A Quantum Dot Single-Photon Turnstile Device. P. Michler, A. Kiraz, C. Becher, W. V. Schoenfeld, P. M. Petroff, Lidong Zhang, E. Hu and A. İmamoğlu in Science 290:2282 (2000).:

This is from Nonclassical radiation from a single self-assembled InAs quantum dot. C. Becher, A. Kiraz, P. Michler, A. İmamoğlu, W. V. Schoenfeld, P. M. Petroff, Lidong Zhang and E. Hu in Phys. Rev. B 63:121312(R) (2001).:

This is from Fast recognition of single molecules based on single-event photon statistics. S. Dong, T. Huang an Y. Liu, J. Wang, Liantuan Xiao G. Zhang and S. Jia in Phys. Rev. A 76:063820 (2007).:

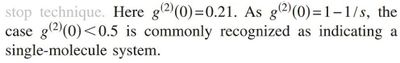
This is from Photon antibunching from a single lithographically defined InGaAs/GaAs quantum dot. V. B. Verma, M. J. Stevens, K. L. Silverman, N. L. Dias, A. Garg, J. J. Coleman and R. P. Mirin in Opt. Express 19:4182 (2011).:

This is from Quantum Statistics of Surface Plasmon Polaritons in Metallic Stripe Waveguides. G. Di Martino, Y. Sonnefraud, S. K\'ena-Cohen, M. Tame, \c S. K. \"Ozdemir, M. S. Kim and S. A. Maier in Nano Lett. 12:2504 (2012). (supplementary material):

This is from Resonance in quantum dot fluorescence in a photonic bandgap liquid crystal host. S. G. Lukishova, L. J. Bissell, J. Winkler and C. R. Stroud in Opt. Lett. 37:1259 (2012).

This is from Bright single-photon sources in bottom-up tailored nanowires. M. E. Reimer, G. Bulgarini, N. Akopian, M. Hocevar, M. Bouwes Bavinck, M. A. Verheijen, E. P.A.M. Bakkers, L. P. Kouwenhoven and V. Zwiller in Nature Comm. 3:737 (2012).:

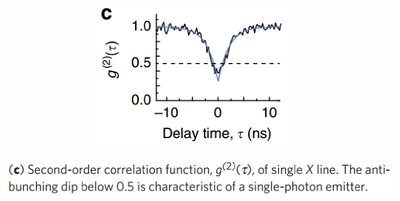
This is from Single-photon experiments with liquid crystals for quantum science and quantum engineering applications. S. G. Lukishova, A. C. Liapis, L. J. Bissell, G. M. Gehring and R. W. Boyd in Liquid Crystals Reviews 2:111 (2014).

This is from Evaluation of nitrogen- and silicon-vacancy defect centres as single photon sources in quantum key distribution. M. Leifgen, T. Schröder, F. Gädeke, R. Riemann, V. Métillon, E. Neu, C. Hepp, C. Arend, C. Becher and K. Lauritsen in New J. Phys. 16:023021 (2014).:

This is from Atomically thin quantum light-emitting diodes. C. Palacios-Berraquero, M. Barbone, D. M. Kara, X. Chen, I. Goykhman, D. Yoon, A. K. Ott, J. Beitner, K. Watanabe, T. Taniguchi, A. C. Ferrari and M. Atatüre in Nature Comm. 7:12978 (2016).:

You also hear it quite a lot in conferences, which is more difficult to reproduce, although you see it in posters too, e.g., this is from Heindel et al. [1]: