The anharmonic oscillator

In Chapter 2, we introduced the Hamiltonian (2.66) of the AO, that includes exciton-exciton interactions when the excitons can still be considered as bosons. Then, interactions manifest as additional energy cost for the multiply-occupied states. The total Hamiltonian for uncoupled interacting excitons is

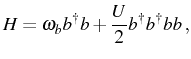$\displaystyle H=\omega_b\ud{b}b+\frac{U}{2}\ud{b}\ud{b}bb\,,$

(5.1)

with

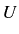
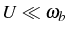
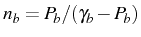
being positive and $U\ll\omega_b$ for weakly repulsive excitons. The steady state of the system under pump and decay (in a thermal bath) is the same (thermal state with $n_b=P_b/(\gamma_b-P_b)$ ) as the harmonic case, as has been shown for example by Scully & Zubairy (2002). The complete dissipative time dynamics has also been obtained analytically, for example by Milburn & (1986). However, in our approach, we concentrate on the correlators and power spectra computed from the complete master equation with pump and decay, for the exciton

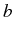
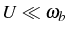
, thanks to the quantum regression formula, as we described in Chapter 2. The results we obtain are physically valid when $U\ll\omega_b$ and the approximations made to derive the master equation hold, as was argued by Alicki (1989). We restrict the discussion to such limits.

In this Section, we see how the simple Hamiltonian spectral structure given by Eq. (2.89) turns into a more complex expression that cannot easily be found analytically.

Subsections