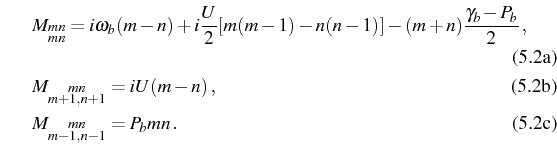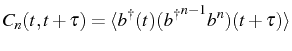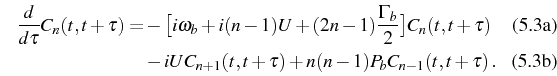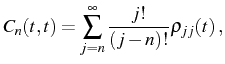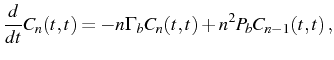First order correlation function and power spectrum

The set of operators that are needed to compute the correlator of interest, namely $\langle\ud{b}(t)b(t+\tau)\rangle$ , are the most general set $\{C_{\{m,n\}}=\ud{b}^mb^n\}$ , differently than for the harmonic oscillator in Section 2.6. The regression matrix is defined by the following rules:

$\begin{subequations}\begin{align}&M_{\substack{mn\\ mn}}=i\omega_b(m-n)+i\frac{U... ...iU(m-n)\,,\\ &M_{\substack{mn\\ m-1,n-1}}=P_bmn\,. \end{align}\end{subequations}$

**Figure 5.1:** Chain of correlators--indexed by $\{\eta\}=(m,n)$ --linked by the Hamiltonian dynamics with pump and decay for one AO. On the left (resp., right), the set $\mathcal{N}_k$ (resp., $\tilde{\mathcal{N}}_k$ ) involved in the equations of the two-time (resp., single-time) correlators. In green is shown the first manifold. The equation of motion $\langle \ud{b}(t)C_{\{\eta\}}(t+\tau)\rangle$ with $\eta\in\mathcal{N}_1$ requires for its initial value the correlator $\langle C_{\{\tilde\eta\}}\rangle$ with $\{\tilde\eta\}\in\tilde{\mathcal{N}}_1$ defined from $\{\eta\}=(m,n)$ by $\{\tilde\eta\}=(m+1,n)$ , as seen on the diagram. The arrows show the connections due to the incoherent pumpings (in green) and the interactions (in red). The sense of the arrows indicates which element is ``calling'' which in its equations. The self-coupling of each node to itself is shown in violet circular arrow (affected by $\omega_b$ , $\Gamma_b$ and ). These links are obtained from the rules in Eq. (5.2a). The dimension of the manifolds is always one. A manifold is only linked directly to $k\pm 1$ in this model.
$\includegraphics[width=.45\linewidth]{chap5/AO/fig1-correlator.ps}$

This gives rise to an infinite set of coupled equations for any general correlator. $\langle\ud{b}(t)b(t+\tau)\rangle$ is linked to all correlators of the kind:

$\displaystyle C_n(t,t+\tau)=\langle\ud{b}(t)(\ud{b}^{n-1}b^n)(t+\tau)\rangle$

(5.3)

with

, 2, ... (see Fig. 5.1), through the general equation:

$\begin{subequations}\begin{align}\frac{d}{d\tau}C_n(t,t+\tau)=&-\big[i\omega_b+i... ...-iUC_{n+1}(t,t+\tau)+n(n-1)P_bC_{n-1}(t,t+\tau)\,. \end{align}\end{subequations}$

$\Gamma_b=\gamma_b-P_b$ is the effective boson broadening, that we have already encountered many times.^5.2Also here, we can write the general equation in a matrix form, $d\mathbf{v}(t,\tau)/d\tau=-\mathbf{M}_1\mathbf{v}(t,\tau)$ where $\mathbf{v}$ is the vector of the ordered correlators $C_n(t,t+\tau)$ (

, 2, ...) and $\mathbf{M}_1$ the corresponding nondiagonal regression matrix extracted from Eq. (5.4). Finally, we integrate $C_n(t,t+\tau)=e^{-\mathbf{M}_1\tau}\,C_n(t,t)$ . The initial average values for the correlators $C_n(t,t)=\langle\ud{b}^nb^n\rangle (t)$ can be found through the density matrix,

$\displaystyle C_n(t,t)=\sum_{j=n}^{\infty}\frac{j!}{(j-n)!}\rho_{jj}(t)\,,$

(5.5)

or applying again the quantum regression formula. The second set of equations,

$\displaystyle \frac{d}{dt}C_n(t,t)=-n\Gamma_bC_n(t,t)+n^2P_bC_{n-1}(t,t)\,,$

(5.6)

are easily solved in the two cases we are interested in. The steady state (SS) is, as we said, the thermal state [Eqs. (2.34)-(2.35)] for which $C_n^\mathrm{SS}=n!n_b^n$ and $n_b=P_b/\Gamma_b$ . The spontaneous decay (SE) from an initial state defined by $C_n^0=\langle\ud{b}^n b^n\rangle (0)$ gives simply $C_n^\mathrm{SE}(t,t)=e^{-n\gamma_b t}C_n^0$ . In both cases, the mean single-time values do not depend on the interactions. They are the same than for the HO.

The correlators $C_n(t,t+\tau)$ cannot be found analytically in the general case with pump because the Hilbert space is infinite ( $n \in [1,\infty)$ ). The formula (2.105) of the spectra must be kept in general terms for the SS emission.

Subsections