Figure 5.2:
SE spectra of emission of the AO (thick
black line) from the state 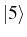 as compared to the HO emission
(a Lorentzian in dashed red). Large interactions (a) help
resolving the five peaks of each transition (thin lines) in the
de-excitation process, while small interactions (b) give
rise to a broad asymmetric peak. The position of the individual
peaks are marked with vertical guide lines at
as compared to the HO emission
(a Lorentzian in dashed red). Large interactions (a) help
resolving the five peaks of each transition (thin lines) in the
de-excitation process, while small interactions (b) give
rise to a broad asymmetric peak. The position of the individual
peaks are marked with vertical guide lines at 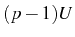 .
. 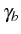 is the unit here and
is the unit here and
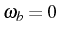 is the reference energy.
is the reference energy.
|
|
The SE case truncates naturally the Hilbert space as the dynamics of
decay only involves states with less number of excitations than the
initial one (
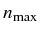 ). Therefore, the solution can be
obtained analytically for the correlator of interest,
). Therefore, the solution can be
obtained analytically for the correlator of interest,
![$\displaystyle C_1^\mathrm{SE}(t,\tau)=e^{-(\omega_b+\gamma_b/2)\tau}\sum_{n=1}^...
...{U}{U-i\gamma_b}(e^{-(iU+\gamma_b)\tau}-1)\right]^{n-1} C_n^\mathrm{SE}(t,t)\,,$](img1318.png) |
(5.7) |
and its spectrum. The parameters that define the Lorentzian,
the dispersive lineshapes and their weight for each peak
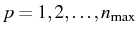
in the expression for the
spectra (
2.105), are:
Figure 5.3:
SS spectra of emission of the AO (thick
black line) as compared to the HO emission (a Lorentzian in dashed
red) for the parameters in inset (all in units of
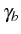 ). In the first row (a)-(c) we fix the
pumping to
). In the first row (a)-(c) we fix the
pumping to
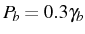 and decrease the interactions, loosing
in resolution of the second and third manifold peaks (thin lines)
and recovering the Lorentzian lineshape. The shifted positions of
the peaks are marked with vertical guide lines in order to compare
with the SE positions
and decrease the interactions, loosing
in resolution of the second and third manifold peaks (thin lines)
and recovering the Lorentzian lineshape. The shifted positions of
the peaks are marked with vertical guide lines in order to compare
with the SE positions 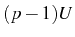 . In the second row
(d)-(f), we fix the interactions to a large
number,
. In the second row
(d)-(f), we fix the interactions to a large
number,
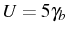 , and increase the pump in order to achieve
, and increase the pump in order to achieve
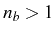 (lasing regime). High manifold transitions melt into
a broad shoulder for the AO while the HO Lorentzian, narrows with
(lasing regime). High manifold transitions melt into
a broad shoulder for the AO while the HO Lorentzian, narrows with
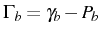 . The shoulder is placed approximately at
. The shoulder is placed approximately at
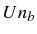 evidencing a transition from a ``quantum'' (with resolved
individual transition) to a ``classical'' (a mean field broad peak)
regime. (f) Contour plot of this effect as a function of
pump (large emission in black). The peak positions,
evidencing a transition from a ``quantum'' (with resolved
individual transition) to a ``classical'' (a mean field broad peak)
regime. (f) Contour plot of this effect as a function of
pump (large emission in black). The peak positions, 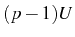 (vertical thin lines), the ever narrowing Lorentzian
(vertical thin lines), the ever narrowing Lorentzian
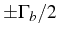 (dashed red) and the value of
(dashed red) and the value of 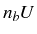 (black thick line), are plotted
for comparison. HO and AO populations diverge in the same way as
pump approaches
(black thick line), are plotted
for comparison. HO and AO populations diverge in the same way as
pump approaches 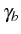 but their spectra is qualitatively very
different, the first one narrowing and the latter effectively
broadening and blueshifting.
but their spectra is qualitatively very
different, the first one narrowing and the latter effectively
broadening and blueshifting. 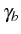 is the unit here and
is the unit here and
 is the reference energy.
is the reference energy.
|
|
The positions and broadenings are reproduced exactly by the manifold
method of Sec. 2.5.2, meaning that we can
associate each individual peak 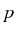 with the transitions from the
manifold with
with the transitions from the
manifold with 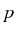 to
to 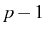 excitations. The peak
excitations. The peak 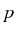 is weighted in
the total spectra by
is weighted in
the total spectra by 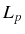 and
and 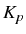 , which are a sum of contributions
from the dynamics of all the states above the ones of the transition,
that is, those from
, which are a sum of contributions
from the dynamics of all the states above the ones of the transition,
that is, those from 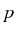 to
to
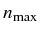 . The only line that
remains at
. The only line that
remains at 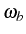 is that corresponding to the decay from the
first manifold, the linear transition with
is that corresponding to the decay from the
first manifold, the linear transition with 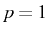 . The rest of lines
are blue-shifted for each manifold
. The rest of lines
are blue-shifted for each manifold 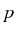 , from
, from 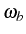 (HO)
to
(HO)
to
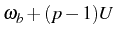 and they are broadened from
and they are broadened from 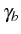 to
to
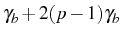 (the higher the manifold, the broader the
peak as compared to the HO), as we can see in
Fig. 5.2 (thin black lines). We consider
(the higher the manifold, the broader the
peak as compared to the HO), as we can see in
Fig. 5.2 (thin black lines). We consider
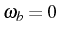 as the reference energy from now on.
as the reference energy from now on.
For large interactions, Fig. 5.2(a), the
individual transitions can be resolved, while, if they are not very
large (
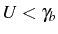 ), they stick together forming a broad asymmetric
peak at the origin, as in Fig. 5.2(b). The
asymmetry may result also in an additional effective blueshift,
noticeable if we compare with the Lorentzian symmetric emission of the
HO (in dashed red).
), they stick together forming a broad asymmetric
peak at the origin, as in Fig. 5.2(b). The
asymmetry may result also in an additional effective blueshift,
noticeable if we compare with the Lorentzian symmetric emission of the
HO (in dashed red).
Elena del Valle
©2009-2010-2011-2012.
![\includegraphics[width=0.47\linewidth]{chap5/AO/SE.eps}](img1312.png)
![\includegraphics[width=0.45\linewidth]{chap5/AO/SE2.eps}](img1313.png)
![]() ). Therefore, the solution can be
obtained analytically for the correlator of interest,
). Therefore, the solution can be
obtained analytically for the correlator of interest,
![\includegraphics[width=0.32\linewidth]{chap5/AO/Fig2a.eps}](img1321.png)
![\includegraphics[width=0.32\linewidth]{chap5/AO/Fig2b.eps}](img1322.png)
![\includegraphics[width=0.32\linewidth]{chap5/AO/Fig2c.eps}](img1323.png)
![\includegraphics[width=0.32\linewidth]{chap5/AO/Fig2d.eps}](img1324.png)
![\includegraphics[width=0.33\linewidth]{chap5/AO/Fig2e.eps}](img1325.png)
![\includegraphics[width=0.32\linewidth]{chap5/AO/Fig3.eps}](img1326.png)
![]() with the transitions from the
manifold with
with the transitions from the
manifold with ![]() to
to ![]() excitations. The peak
excitations. The peak ![]() is weighted in
the total spectra by
is weighted in
the total spectra by ![]() and
and ![]() , which are a sum of contributions
from the dynamics of all the states above the ones of the transition,
that is, those from
, which are a sum of contributions
from the dynamics of all the states above the ones of the transition,
that is, those from ![]() to
to
![]() . The only line that
remains at
. The only line that
remains at ![]() is that corresponding to the decay from the
first manifold, the linear transition with
is that corresponding to the decay from the
first manifold, the linear transition with ![]() . The rest of lines
are blue-shifted for each manifold
. The rest of lines
are blue-shifted for each manifold ![]() , from
, from ![]() (HO)
to
(HO)
to
![]() and they are broadened from
and they are broadened from ![]() to
to
![]() (the higher the manifold, the broader the
peak as compared to the HO), as we can see in
Fig. 5.2 (thin black lines). We consider
(the higher the manifold, the broader the
peak as compared to the HO), as we can see in
Fig. 5.2 (thin black lines). We consider
![]() as the reference energy from now on.
as the reference energy from now on.
![]() ), they stick together forming a broad asymmetric
peak at the origin, as in Fig. 5.2(b). The
asymmetry may result also in an additional effective blueshift,
noticeable if we compare with the Lorentzian symmetric emission of the
HO (in dashed red).
), they stick together forming a broad asymmetric
peak at the origin, as in Fig. 5.2(b). The
asymmetry may result also in an additional effective blueshift,
noticeable if we compare with the Lorentzian symmetric emission of the
HO (in dashed red).


![$\displaystyle C_1^\mathrm{SE}(t,\tau)=e^{-(\omega_b+\gamma_b/2)\tau}\sum_{n=1}^...
...{U}{U-i\gamma_b}(e^{-(iU+\gamma_b)\tau}-1)\right]^{n-1} C_n^\mathrm{SE}(t,t)\,,$](img1318.png)
![\begin{subequations}\begin{align}&\omega_p=\omega_b+(p-1)U\,,\\ [.3cm] &\gamma_p...
...1}}{n (n-p-2)!}C_n^0\,. <tex2html_comment_mark>564 \end{align}\end{subequations}](img1320.png)