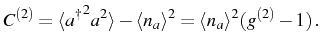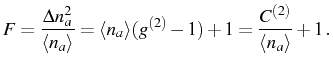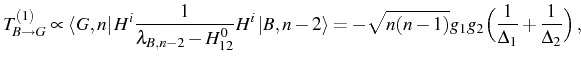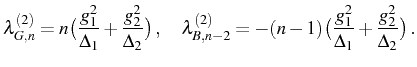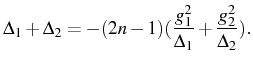Two-photon lasing

The last effect we consider with this configuration is the two-photon lasing. Two-photon (2P) related effects have been extensively studied, and observed in many configurations, during the past few decades. We first list here the most relevant works for our discussion.

Two-photon masers have been theoretically described by Davidovich et al. (1987), and Ashraf et al. (1990) and engineered by Brune et al. (1987). Atoms (effective three level systems) were injected in a cavity in the upper level of a transition which was 2P-resonant with the cavity mode. The state of the atoms was time-resolved and it was found that above threshold the lower state of the 2P transition was populated, evidencing the 2P de-excitation. This effect is present only for a small range of cavity detunings around the 2P resonance (2PR). The same principle applies for the case of a single few-level atom when the quality factor of the cavity, , is sufficiently increased.

Lewenstein et al. (1990) studied theoretically 2P gain and lasing. This was achieved experimentally by Gauthier et al. (1992) in an ensemble of many atoms (2LSs) strongly driven by a continuous laser. The system can undergo a 2P transition between dressed states (arising from the laser-atoms coupling) if this transition is enhanced by also coupling the atoms to a cavity mode. The 1 and 2 photon lasing regimes are switched on and off by tuning the cavity energy, taking into account the Stark shift and triggering the 2P lasing with a cw probe. The two regimes are distinguished mainly thanks to the cavity energy at which the output intensity is enhanced. The main experimental point to claim a 2P based laser is the appearance of an extra peak in the emission at the 2PR. This peak grows on top of the one photon (1P) emission, that otherwise does not lase at this energy. In this configuration there is an intrinsic superposition of both 1 and 2P processes that, in the best of cases, can be optimized so that the 2P gain is dominant. Recently, Kubanek et al. (2008) realized experimentally a two-photon gateway with a single atom, in a similar scheme. In their experiment, dressed states appear due to the strong coupling between the atom and the cavity. A weak cw laser field is shined on the system providing photons that are absorbed and emitted in pairs when there is a 2PR with manifold 2 [see Fig. 5.12 (c)]. The quantity used here to evidence that such process dominates the off-resonant 1P counterpart, is the so-called differential correlation function at zero delay, $C^{(2)}$ , which is a variation of $g^{(2)}$ :

$\displaystyle C^{(2)}=\langle\ud{a}^2a^2\rangle -\langle n_a\rangle ^2=\langle n_a\rangle ^2(g^{(2)}-1)\,.$

(6.17)

As explained by Kubanek et al. (2008), $C^{(2)}$ reflects better the 2P versus 1P probability competition than $g^{(2)}$ and we will prefer it in this context. Another interesting quantity found in the literature (see, for instance, Koganov & (2000)), is the Fano factor:

$\displaystyle F=\frac{\Delta n_a^2}{\langle n_a\rangle }=\langle n_a\rangle (g^{(2)}-1)+1=\frac{C^{(2)}}{\langle n_a\rangle }+1\,.$

(6.18)

The two-photon dynamics has also been explored theoretically for two atoms (two 2LSs) interacting with a driving laser by Varada & (1992) or with a cavity mode (as here) by Pathak & (2004). In both cases, the light mode was considered to be far from resonance, with any of the single atom energies but close to resonance with their sum. In order to avoid the destructive interference between the two possible 2P de-excitation paths that can occur from state $\ket{B}$ (through $\ket{E1}$ or $\ket{E2}$ ), different ideas can be implemented. Varada & (1992) added dipole-dipole direct interactions between the dots and a 2PR was found even for two identical atoms. The 2P absorption and spontaneous emission were characterized by their intensity at the 2PR, and also by the probability that both atoms are excited (related to the transition probability for 2P absorption). The problem of the competition with the 1P processes was not addressed in this work where it was taken for granted that the system is completely dominated by 2P processes. Pathak & (2004) removed the two-path interference by considering either two different atomic levels (different detunings $\vert\Delta_1\vert\neq\vert\Delta_2\vert$ and couplings $g_1\neq g_2$ ) or two different cavity modes. The authors concentrated on the Hamiltonian dynamics looking into 2P versus 1P Rabi oscillations of the wavefunction. Lambropoulos (1999) also considered two cavity modes, each one associated with the 1P or 2P lasing, coupled and resonant with two different atomic transitions separately. Here, an incoherent continuous pump for the atoms was considered that inverted the population of the 2P transition. A comparison of the intensity emitted in each mode allowed to quantify the 2P efficiency.

In most of the cases just described, the Stark shift induced by the off-resonant 1P exchange with the atomic levels is taken into account in order to achieve a real 2PR in the system. The 2P lasing is simply characterized by the enhancement in the intensity of the emission at the 2PR against that achieved at the 1PR. This could be observed in continuous operation or thanks to time-resolved measurements of the dynamics after a probe. In the case of coherent excitation of the atoms or spontaneous emission from the excited state, the population of the atomic levels can also be a meaningful magnitude.

The configuration we are investigating is that of Pathak & (2004), in the SS under incoherent continuous pump. In this system, a 2PR can be induced when $\omega_1+\omega_2\approx 2\omega_a$ . At the same time, in order to suppress one photon processes, the single exciton energies should be greatly detuned from the cavity mode. The unperturbed states $\ket{G,n}$ and $\ket{B,n-2}$ are resonant if $\Delta_1=-\Delta_2$ . However in this case the two photon transition probability is zero due to destructive interference between the processes $\ket{B,n-1}\to\ket{E1,n-1}\to\ket{G,n}$ and $\ket{B,n-1}\to\ket{E2,n-1}\to\ket{G,n}$ . That is, the transition probability to first order in the small parameter $g_j/\vert\Delta_2-\Delta_1\vert$ ,

$\displaystyle T^{(1)}_{B\to G}\propto\bra{G,n}H^i\frac{1}{\lambda_{B,n-2}-H_{12... ...t{B,n-2}=-\sqrt{n(n-1)}g_1g_2\Big(\frac{1}{\Delta_1}+\frac{1}{\Delta_2}\Big)\,,$

(6.19)

is zero in this case, even when the couplings are different. By keeping $\vert\Delta_1\vert\neq\vert\Delta_2\vert$ , second order resonant 2P Rabi oscillations can become larger than the first order off-resonance 1P oscillations as detunings are increased with opposite signs. An example of such a situation is plotted in Fig. 6.14. The 2P oscillations (between the blue and the brown lines) are slightly dominant over the 1P ones (in purple).

**Figure 6.14:** Populations of the QD levels as a function of time with initial state $\ket{B,0}$ in the 2PR: $\ket{B,0}$ (solid-blue line), $\ket{E,1}$ (dashed-purple) and $\ket{G,2}$ (dotted-brown). The parameters are those of Pathak & (2004): , $\Delta_1=5g_1$ , $\Delta_2=-2.8g_1$ . The oscillations take place in the second manifold, mainly between $\ket{B,0}$ and $\ket{G,2}$ , with the exchange of two photons.
$\includegraphics[width=0.75\linewidth]{chap6/2P/Levels/resonance-pathak.eps}$

We evaluate the corrections at second order in perturbation theory to the two bare energies as done in the book by Cohen-Tannoudji et al. (2001), which are the so-called Stark shifts:

$\displaystyle \lambda_{G,n}^{(2)}=n\big(\frac{g_1^2}{\Delta_1}+\frac{g_2^2}{\De... ..._{B,n-2}^{(2)}=-(n-1)\big(\frac{g_1^2}{\Delta_1}+\frac{g_2^2}{\Delta_2}\big)\,.$

(6.20)

The corresponding eigenenergies for the system with

excitations are $E_{\alpha}=n\omega_0+\lambda_\alpha^{0}+\lambda_\alpha^2$ . The condition for resonant two-photon emission $E_{B,n-2}=E_{G,n}$ becomes

$\displaystyle \Delta_1+\Delta_2=-(2n-1)(\frac{g_1^2}{\Delta_1}+\frac{g_2^2}{\Delta_2}).$

(6.21)

When this condition is satisfied the transfer of population between state $\ket{B,n-2}$ and $\ket{G,n}$ is almost perfect with negligible excitation of the intermediate states $\ket{E1,n-1}$ and $\ket{E2,n-1}$ .

Already at this Hamiltonian level, it is complicated to fit the above 2PR condition while keeping large detunings to suppress the 1PR. The 2PR condition demands detunings with opposite signs whose absolute value is close to each other but still different. Therefore, either 2PR is fulfilled but with the 1PR also strongly present (for not so large a detuning as in the case of Pathak & (2004), in Fig. 6.14) either the 1PR is completely suppressed but the 2P oscillations are weak and occur very slowly as it corresponds to a 4th order effect (when detunings are large and almost equal).

Moreover, the 2P effect is so weak that in a realistic environment is overcome by decoherence and not observable. Note as well that the resonance condition depends on the number of photons . Therefore the 2P emission can be efficient only for a fixed . When pump and decay mechanisms drive the system, several manifolds of different number of excitations enter the dynamics and the condition can only be fulfilled partially. This is why we will explore other possibilities for 2P generation in the rest of the Chapter.