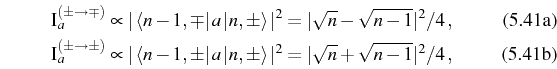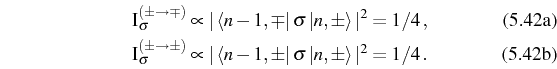Point 1: very good systems and the incoherent Mollow triplet
Point 1, is best suited to explore quantum effects. Its spectral shape
is unambiguously evidencing transitions in the Jaynes-Cummings ladder,
as shown in Fig. 5.17 with a clear
``Jaynes-Cummings fork'' (a quadruplet). The outer peaks at ![]() are the conventional vacuum Rabi doublet, whereas the two inner peaks
correspond to higher transitions in the ladder. Observation of a
transition from outer to inner peaks with pumping such as shown in
Fig. 5.17 would be a compelling evidence of
a quantum exciton in SC with the
cavity. Fig. 5.18 shows another multiplet
structure of this kind for Point 1. The intensity of emission is
presented in log-scale and for a broader range of frequencies, so that
small features can be revealed. Transitions from up to the third
manifold can be explicitly identified. The decay from the second
manifold, that manifests distinctly with peaks labelled 2 (although it
also contributes to peaks labelled 0), is already weak but still might
be identifiable in an experimental PL measurement. Higher transitions
have decreasing strenght. This can be checked with the probability to
have
are the conventional vacuum Rabi doublet, whereas the two inner peaks
correspond to higher transitions in the ladder. Observation of a
transition from outer to inner peaks with pumping such as shown in
Fig. 5.17 would be a compelling evidence of
a quantum exciton in SC with the
cavity. Fig. 5.18 shows another multiplet
structure of this kind for Point 1. The intensity of emission is
presented in log-scale and for a broader range of frequencies, so that
small features can be revealed. Transitions from up to the third
manifold can be explicitly identified. The decay from the second
manifold, that manifests distinctly with peaks labelled 2 (although it
also contributes to peaks labelled 0), is already weak but still might
be identifiable in an experimental PL measurement. Higher transitions
have decreasing strenght. This can be checked with the probability to
have ![]() photons in the cavity,
photons in the cavity,
![]() , computed from
Eqs. (5.13). Whenever the mean number
, computed from
Eqs. (5.13). Whenever the mean number ![]() is low (as is the case here), this probability is maximum for the
vacuum (
is low (as is the case here), this probability is maximum for the
vacuum (
![]() for all
for all ![]() ), independently of
the nature of the photon distribution (sub, super or Poissonian). Only
when
), independently of
the nature of the photon distribution (sub, super or Poissonian). Only
when ![]() , in the best of cases (for a Poissonian distribution),
does this trend start to invert and
, in the best of cases (for a Poissonian distribution),
does this trend start to invert and
![]() .
.
![\includegraphics[width=.45\linewidth]{chap5/JC/fig7-jc-fork.ps}](img1641.png) |
![\includegraphics[width=.66\linewidth]{chap5/JC/fig8-jc-multiplets.ps}](img1643.png) |
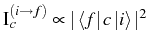 ,
estimates the relative intensity of the peaks depending on the
initial,
,
estimates the relative intensity of the peaks depending on the
initial, evidence the predominance of the inner peaks versus the outer ones, given that one expect the same weighting of both transitions from the dynamics of the system. The doublet formed by the inner peaks is therefore strong and clearly identifiable in an experiment. On the other hand, in the direct exciton emission, the counterparts of Eqs. (5.43) are manifold-independent and equal for both the inner and outer peaks:
In this case, therefore, one can expect similar strength of transitions for both the inner and outer peaks with a richer multiplet structure for the direct exciton emission.
In Fig. 5.19, we give an overview of the PL
spectra as ![]() is varied from very small to very large
values. For point 1, as we already noted, the cavity pumping plays a
relatively minor quantitative role. Therefore we only show two cases,
of no-cavity pumping (first row) and high-cavity pumping (second
row). As can be seen, there is no strong difference from one spectra
with no cavity pumping to its counterpart with large cavity
pumping. Third row shows the direct exciton emission that, with no
cavity pumping, corresponds to the first row. Indeed, one can observe
the richer multiplet structure up to
is varied from very small to very large
values. For point 1, as we already noted, the cavity pumping plays a
relatively minor quantitative role. Therefore we only show two cases,
of no-cavity pumping (first row) and high-cavity pumping (second
row). As can be seen, there is no strong difference from one spectra
with no cavity pumping to its counterpart with large cavity
pumping. Third row shows the direct exciton emission that, with no
cavity pumping, corresponds to the first row. Indeed, one can observe
the richer multiplet structure up to
![]() in the
direct exciton emission, whereas only inner peaks are neatly manifest
in the cavity emission. This region corresponds to a quantum regime
with a few quanta of excitations (and subpoissonian particle number
distribution,
in the
direct exciton emission, whereas only inner peaks are neatly manifest
in the cavity emission. This region corresponds to a quantum regime
with a few quanta of excitations (and subpoissonian particle number
distribution, ![]() ) giving rise to clearly resolvable peaks,
attributable to the Hamiltonian manifolds. Therefore, a good system
(high
) giving rise to clearly resolvable peaks,
attributable to the Hamiltonian manifolds. Therefore, a good system
(high ![]() and
and ![]() ) and a good QD (two-level) emitter suffice to easily
and clearly observe quantum effects. There is no need of pumping
harder than it has been done in present systems so far.
) and a good QD (two-level) emitter suffice to easily
and clearly observe quantum effects. There is no need of pumping
harder than it has been done in present systems so far.
![\includegraphics[width=\linewidth]{chap5/JC/fig10-SpecsPt1details.ps}](img1660.png) |
In the region
![]() , the photon fluctuations are those of a
coherent, classical state,
, the photon fluctuations are those of a
coherent, classical state, ![]() . Increasing pumping with the
intention to penetrate further into the nonlinearity, merely collapses
the multiplet structure into a single line, as far as cavity emission
is concerned. However, this does not mean that the system is in weak
coupling. In the direct exciton emission, the rich SC fine structure
has turned into a Mollow triplet, like the one found by
Mollow (1969), that we discuss in depth below. In this
region, the first manifolds have crossed to WC but higher manifolds
retain SC, bringing the system into lasing. At this point, a change of
realm should be performed favoring a classical description, as we
already pointed out with the AO. A last transition into thermal light
and WC, due to saturation and self-quenching, takes place at
. Increasing pumping with the
intention to penetrate further into the nonlinearity, merely collapses
the multiplet structure into a single line, as far as cavity emission
is concerned. However, this does not mean that the system is in weak
coupling. In the direct exciton emission, the rich SC fine structure
has turned into a Mollow triplet, like the one found by
Mollow (1969), that we discuss in depth below. In this
region, the first manifolds have crossed to WC but higher manifolds
retain SC, bringing the system into lasing. At this point, a change of
realm should be performed favoring a classical description, as we
already pointed out with the AO. A last transition into thermal light
and WC, due to saturation and self-quenching, takes place at
![]() that leads to a single central peak in the
spectra.
that leads to a single central peak in the
spectra.
![\includegraphics[width=\linewidth]{chap5/JC/fig11-mollow-triplet.ps}](img1666.png) |
In Fig. 5.20, we take a closer look into
Fig. 5.19 in the region of the loss of the
doublet of inner peaks with increasing electronic pumping, where the
system starts to cross from the quantum to the classical regime. In
the cavity emission, the doublet of inner peaks collapses into a
single line that is going to narrow as the system lases. At the same
time, a strikingly richer structure and regime transition is observed
in the direct exciton emission. As the peaks are more clearly resolved
as explained before [cf. Eqs. (5.43)
and (5.44)], the ``melting'' of the
Jaynes-Cummings ladder into a classical structure is better tracked
down. Indeed, as pumping is increased, broadening of these lines
starts to unite them together into an emerging structure of a much
less reduced complexity, namely a triplet. This is completely
equivalent to the transition from quantum to classical AO that we
studied in Sec. 5.2. In
Fig. 5.21, we provide another zoom of the
overall picture given by Fig. 5.19, this
time for the direct exciton emission exclusively. First three rows
show the evolution with electronic pumping ![]() (values in
inset) over a wide range of frequencies, up to
(values in
inset) over a wide range of frequencies, up to ![]() , while the
three last rows show the very same spectra, with a one-to-one mapping
with previous rows, only in the range of frequencies
, while the
three last rows show the very same spectra, with a one-to-one mapping
with previous rows, only in the range of frequencies ![]() . The
transition manifests to different scales, with a rich fine multiplet
structure in the quantum regime, as seen in the zoomed-in region, to a
monolithic triplet at higher pumpings, as seen in the enlarged
region. On the right, spectra are superimposed to follow their
evolution with pumping. The two broad satellites peaks, at
approximately
. The
transition manifests to different scales, with a rich fine multiplet
structure in the quantum regime, as seen in the zoomed-in region, to a
monolithic triplet at higher pumpings, as seen in the enlarged
region. On the right, spectra are superimposed to follow their
evolution with pumping. The two broad satellites peaks, at
approximately
![]() (in the AO the broad peak was placed at
(in the AO the broad peak was placed at
![]() ), drift apart from the main central one with increasing
excitation, and in this sense behave as expected from a Mollow
triplet. Various deviations are however observed, of a more or less
striking character. The most astonishing feature is the emergence of a
very sharp and narrow peak in the center, that has been plotted with
its total intensity on the right panel to give a sense of its
magnitude. It is clearly seen in the zoomed-region how this peak
arises on top of the broad mountain of inner peaks, surviving the
collapse of the fine structure in the classical regime. This thin
central resonance appears when a large truncation is needed. It is a
sum of many contributing peaks centered at zero, most of them with
very small intensities. This region therefore shows all the signs of a
transition from a quantum to a classical system. At low pumping, the
inner peaks of all quadruplets coming from low order manifolds are
placed approximately at
), drift apart from the main central one with increasing
excitation, and in this sense behave as expected from a Mollow
triplet. Various deviations are however observed, of a more or less
striking character. The most astonishing feature is the emergence of a
very sharp and narrow peak in the center, that has been plotted with
its total intensity on the right panel to give a sense of its
magnitude. It is clearly seen in the zoomed-region how this peak
arises on top of the broad mountain of inner peaks, surviving the
collapse of the fine structure in the classical regime. This thin
central resonance appears when a large truncation is needed. It is a
sum of many contributing peaks centered at zero, most of them with
very small intensities. This region therefore shows all the signs of a
transition from a quantum to a classical system. At low pumping, the
inner peaks of all quadruplets coming from low order manifolds are
placed approximately at
![]() . Even when
they are summed up to produce the total spectrum, the nonlinear
doublet is still resolved. At around
. Even when
they are summed up to produce the total spectrum, the nonlinear
doublet is still resolved. At around
![]() ,
manifolds high enough are excited so that for them
,
manifolds high enough are excited so that for them
![]() . This is a feature of a classical
field resulting in a Mollow triplet. Note that nothing of this sort
is observed in the cavity emission. The Mollow triplet, whether in
atomic physics with coherent excitation or in semiconductor physics
with incoherent pumping, is a feature of the quantum emitter itself,
when it is directly probed. There is therefore a strong motivation
here to detect leak emission of semiconductor structures. The overall
features of this ``incoherent Mollow triplet'' differ from its
counterpart namesake in the strong asymmetry of the satellites and
their increased broadenings with pumping.
. This is a feature of a classical
field resulting in a Mollow triplet. Note that nothing of this sort
is observed in the cavity emission. The Mollow triplet, whether in
atomic physics with coherent excitation or in semiconductor physics
with incoherent pumping, is a feature of the quantum emitter itself,
when it is directly probed. There is therefore a strong motivation
here to detect leak emission of semiconductor structures. The overall
features of this ``incoherent Mollow triplet'' differ from its
counterpart namesake in the strong asymmetry of the satellites and
their increased broadenings with pumping.
In order to appreciate more precisely the structure of the Mollow
triplet and how it emerges from the quantum regime, we consider a even
better system than Point 1: ![]() of the order of
of the order of ![]() ,
,
![]() and
and
![]() . With very small pumping rates, in
Fig 5.22 we can see the very sharp (owing to
the small decay rates) individual lines from each transition. In the
plot of the cavity emission, Fig 5.22
. With very small pumping rates, in
Fig 5.22 we can see the very sharp (owing to
the small decay rates) individual lines from each transition. In the
plot of the cavity emission, Fig 5.22![]() ,
we have marked each peak with its corresponding transition between two
quantized, dressed states of the JC Hamiltonian. These peaks
correspond one-to-one with those of the exciton emission, that are, as
we just explained, weighted differently. In both cases, the Rabi
doublet dominates strongly over the other peaks. In
Fig. 5.22
,
we have marked each peak with its corresponding transition between two
quantized, dressed states of the JC Hamiltonian. These peaks
correspond one-to-one with those of the exciton emission, that are, as
we just explained, weighted differently. In both cases, the Rabi
doublet dominates strongly over the other peaks. In
Fig. 5.22![]() , for instance, the peaks
at
, for instance, the peaks
at ![]() extend for about 9 times higher than is shown, and already
the outer transitions are barely noticeable. This is because the
pumping is small and so also the probability of having more than one
photon in the cavity (it is in this configuration of about 10% to
have
extend for about 9 times higher than is shown, and already
the outer transitions are barely noticeable. This is because the
pumping is small and so also the probability of having more than one
photon in the cavity (it is in this configuration of about 10% to
have ![]() photons, see Fig. 5.25). One could
spectrally resolve the window
photons, see Fig. 5.25). One could
spectrally resolve the window
![]() over a long integration
time and obtain the multiplet structure of nonlinear inner peaks, with
spacings
over a long integration
time and obtain the multiplet structure of nonlinear inner peaks, with
spacings
![]() (in units of
(in units of ![]() ), observing
direct manifestation of single photons renormalizing the quantum
field. Or one could increase pumping (as we do later) or use a cavity
with smaller lifetime. In this case, less peaks of the JC transitions
are observable because of broadenings mixing them together, dephasing
and, again, reduced probabilities for the excited states, but the
balance between them is better. In
Fig. 5.23, where
), observing
direct manifestation of single photons renormalizing the quantum
field. Or one could increase pumping (as we do later) or use a cavity
with smaller lifetime. In this case, less peaks of the JC transitions
are observable because of broadenings mixing them together, dephasing
and, again, reduced probabilities for the excited states, but the
balance between them is better. In
Fig. 5.23, where ![]() is now
is now ![]() ,
the vacuum Rabi doublet (marked
,
the vacuum Rabi doublet (marked ![]() ) is dominated by the nonlinear
inner peaks in the cavity emission, and a large sequence of peaks is
resolved in the exciton emission.
) is dominated by the nonlinear
inner peaks in the cavity emission, and a large sequence of peaks is
resolved in the exciton emission.
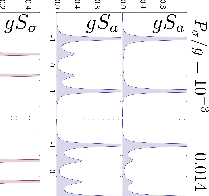
Going back to the case of Fig. 5.22, but
increasing pumping, we observe the effect of climbing higher the
Jaynes-Cummings ladder. Results are shown in
Fig. 5.24 in logarithmic scale, so that
small features are magnified. First row is
Fig. 5.22 again but in log-scale, so that
the effect of this mathematical magnifying glass can be
appreciated. Also, we plot over the wider range
![]() . Note how
the fourth outer peak, that was not visible on the linear scale, is
now comfortably revealed with another three peaks at still higher
energies. As pumping is increased, we observe that the strong Rabi
doublet is receding behind nonlinear features, with more manifolds
indeed being probed, with their corresponding transitions clearly
observed (one can track up to the 19th manifold in the last row). This
demonstrates obvious quantization in a system with a large number of
photons. The distribution of photons in these three cases is given in
Fig. 5.25, going from a thermal-like, mostly
dominated by vacuum, distribution, to coherent-like, peaked
distribution stabilizing a large number of particles in the system.
At the same time, note the cumulative effect of all the side peaks
from the higher manifolds excitations, absorbing all quantum
transitions into a background that is building up shoulders, with the
overall structure of a triplet. This is the mechanism through which
the system bridges from a quantum to a classical system with the
Mollow triplet. These are obtained this time, both in the cavity and
the exciton emission, but much more so in the latter.
. Note how
the fourth outer peak, that was not visible on the linear scale, is
now comfortably revealed with another three peaks at still higher
energies. As pumping is increased, we observe that the strong Rabi
doublet is receding behind nonlinear features, with more manifolds
indeed being probed, with their corresponding transitions clearly
observed (one can track up to the 19th manifold in the last row). This
demonstrates obvious quantization in a system with a large number of
photons. The distribution of photons in these three cases is given in
Fig. 5.25, going from a thermal-like, mostly
dominated by vacuum, distribution, to coherent-like, peaked
distribution stabilizing a large number of particles in the system.
At the same time, note the cumulative effect of all the side peaks
from the higher manifolds excitations, absorbing all quantum
transitions into a background that is building up shoulders, with the
overall structure of a triplet. This is the mechanism through which
the system bridges from a quantum to a classical system with the
Mollow triplet. These are obtained this time, both in the cavity and
the exciton emission, but much more so in the latter.
![\includegraphics[width=\linewidth]{chap5/ICTOPON/spec1.ps}](img1679.png) |
![\includegraphics[width=\linewidth]{chap5/ICTOPON/spec2.ps}](img1681.png) |
![\includegraphics[width=\linewidth]{chap5/ICTOPON/specs3.ps}](img1683.png) |
![\includegraphics[width=.5\linewidth]{chap5/ICTOPON/distribution.ps}](img1684.png) |
Elena del Valle ©2009-2010-2011-2012.