Population and Statistics
To know which features of the spectral structure dominate and which
are negligible, one needs to know what is the quantum state of the
system. In the LM, it was enough to know the average photon (![]() )
and exciton (
)
and exciton (![]() ) numbers, and the off-diagonal
element
) numbers, and the off-diagonal
element
![]() . In the two 2LS, only one more
averaged quantity,
. In the two 2LS, only one more
averaged quantity, ![]() , was necessary. In the most general case of
the fermion system, a countably infinite number of parameters are
required for the exact lineshape, as in the LM with interactions or
the AO. The new order of complexity brought by the fermion system is
illustrated for even the simplest observable. Instead of a closed
relationship that provides, e.g., the populations in terms of the
system parameters and pumping rates, only relations between
observables can be obtained in the general case. For instance, for the
populations:
, was necessary. In the most general case of
the fermion system, a countably infinite number of parameters are
required for the exact lineshape, as in the LM with interactions or
the AO. The new order of complexity brought by the fermion system is
illustrated for even the simplest observable. Instead of a closed
relationship that provides, e.g., the populations in terms of the
system parameters and pumping rates, only relations between
observables can be obtained in the general case. For instance, for the
populations:
This expression is formally the same as for the coupling of two bosonic modes. The differences are in the effective dissipation parameter
When
![]() , we get the following bounds for the cavity
populations in terms of the system and pumping parameters:
, we get the following bounds for the cavity
populations in terms of the system and pumping parameters:
When
If Eq. (5.38) is not fulfilled, the system diverges, as more particles are injected at all times by the incoherent cavity pumping than are lost by decay. Numerical evidence suggests that the actual maximum value of
The second order correlator ![]() at zero delay can be expressed
as a function of
at zero delay can be expressed
as a function of ![]() only:
only:
Obtaining the expression for the
![\includegraphics[width=.75\linewidth]{chap5/JC/fig3-parameters-qd.ps}](img1583.png) |
![\includegraphics[width=\linewidth]{chap5/JC/fig4-averages.ps}](img1590.png) |
As an overall representation of the typical systems that arise in real
and desired experiments, we consider three configurations, shown in
Fig. (5.13), scattered in order to give a rough
representative picture of the overall possibilities, around parameters
estimated by Khitrova et al. (2006). Point 1 corresponds to the
best system of our selection, in the sense that its decay rates are
very small (
![]() ,
,
![]() ), and the quantum
(Hamiltonian) dynamics dominates largely the system. It is a system
still outside of the experimental reach. Point 3 on the other hand
corresponds to a cavity with important dissipations, that, following
our analysis below, precludes the observation of any neat structure
attributable to the underlying Fermi statistics. According to
numerical fitting of the experiment, real structures might even be
suffering higher dissipation rates (see
Sec. 3.5). Point 2 represents other lead
systems of the SC physics, that we will show can presents strong
departure from the linear regime, in particular conditions that we
will emphasize. The best semiconductor system from
Fig. 5.13 is realized with microdisks, thanks
to the exceedingly good cavity factors. We shall not enter into
specific discussion of the advantages and inconvenient of the
respective realizations and the accuracy of these estimations. From
now on, we shall refer to this set of parameters as that of
``reference points'', keeping in mind that points 1 and 2 in
particular represent systems that we will refer to as a ``good
system'' and a ``more realistic system'', respectively.
), and the quantum
(Hamiltonian) dynamics dominates largely the system. It is a system
still outside of the experimental reach. Point 3 on the other hand
corresponds to a cavity with important dissipations, that, following
our analysis below, precludes the observation of any neat structure
attributable to the underlying Fermi statistics. According to
numerical fitting of the experiment, real structures might even be
suffering higher dissipation rates (see
Sec. 3.5). Point 2 represents other lead
systems of the SC physics, that we will show can presents strong
departure from the linear regime, in particular conditions that we
will emphasize. The best semiconductor system from
Fig. 5.13 is realized with microdisks, thanks
to the exceedingly good cavity factors. We shall not enter into
specific discussion of the advantages and inconvenient of the
respective realizations and the accuracy of these estimations. From
now on, we shall refer to this set of parameters as that of
``reference points'', keeping in mind that points 1 and 2 in
particular represent systems that we will refer to as a ``good
system'' and a ``more realistic system'', respectively.
In Fig. 5.14, the three observable of main
interest for a physical understanding of the system that we have just
discussed--![]() ,
, ![]() and
and ![]() --are obtained numerically
for the three reference points. Electronic pumping is varied from,
for all practical purposes, vanishing (
--are obtained numerically
for the three reference points. Electronic pumping is varied from,
for all practical purposes, vanishing (![]() ) to infinite
(
) to infinite
(![]() ) values. Various cavity pumpings are investigated and
represented by the color code from no-cavity pumping (dark blue) to
high, near diverging, cavity pumping (red), through the color
spectrum. We checked numerically that these results
satisfy Eq. (5.36). The overall behavior
is mainly known, for instance the characteristic increase till a
maximum and subsequent decrease of
) values. Various cavity pumpings are investigated and
represented by the color code from no-cavity pumping (dark blue) to
high, near diverging, cavity pumping (red), through the color
spectrum. We checked numerically that these results
satisfy Eq. (5.36). The overall behavior
is mainly known, for instance the characteristic increase till a
maximum and subsequent decrease of ![]() with
with ![]() has been
predicted in a system of QD coupled to a microsphere
by Benson & (1999). This phenomenon of so-called
self-quenching is due to the excitation impairing the coherent
coupling of the dot with the cavity: bringing in an exciton too early
disrupts the interaction between the exciton-photon pair formed from
the previous exciton. Therefore the pumping rate should not overcome
significantly the coherent dynamics. Too high electronic pumping
forces the QD to remain in its excited state and thereby prevents it
from populating the cavity. In this case the cavity population returns
to zero while the exciton population (or probability for the QD to be
excited) is forced to one. This effect appeared as well in the two
2LSs, with the quenching of the direct emission when the dots
saturated with the excitonic pump. The cavity pumping brings an
interesting extension to this mechanism. First there is no quenching
for the pumping of bosons that, on the contrary, have a natural
tendency to accumulate and lead to a divergence. Therefore the
limiting values for
has been
predicted in a system of QD coupled to a microsphere
by Benson & (1999). This phenomenon of so-called
self-quenching is due to the excitation impairing the coherent
coupling of the dot with the cavity: bringing in an exciton too early
disrupts the interaction between the exciton-photon pair formed from
the previous exciton. Therefore the pumping rate should not overcome
significantly the coherent dynamics. Too high electronic pumping
forces the QD to remain in its excited state and thereby prevents it
from populating the cavity. In this case the cavity population returns
to zero while the exciton population (or probability for the QD to be
excited) is forced to one. This effect appeared as well in the two
2LSs, with the quenching of the direct emission when the dots
saturated with the excitonic pump. The cavity pumping brings an
interesting extension to this mechanism. First there is no quenching
for the pumping of bosons that, on the contrary, have a natural
tendency to accumulate and lead to a divergence. Therefore the
limiting values for ![]() when
when
![]() or
or
![]() are not zero, as in the previously
reported self-quenching scenario. They also happen to be different:
are not zero, as in the previously
reported self-quenching scenario. They also happen to be different:
and therefore satisfy
for the cavity, and
In the works of Mu & (1992), Ginzel et al. (1993), Jones et al. (1999),
Karlovich & (2001) or Kozlovskii & (1999), important application
of SC for single-atom lasing were found for good cavities 1 and 2,
where the coupling
![]() is strong enough. Lasing
can occur when the pumping is also large enough to overcome the total
losses,
is strong enough. Lasing
can occur when the pumping is also large enough to overcome the total
losses,
![]() . Setting
. Setting ![]() ,
,
![]() , Eqs. (5.13) can be
approximately reduced to one for the total photonic probability
, Eqs. (5.13) can be
approximately reduced to one for the total photonic probability
![]() , as it has been shown by Scully & Zubairy (2002) or
Benson & (1999):
, as it has been shown by Scully & Zubairy (2002) or
Benson & (1999):
The parameters that characterize the laser are the gain
The effect of cavity pumping depends strongly on the experimental
situation. In the case of an exceedingly good system, ![]() has little
effect as soon as the exciton pumping is important,
has little
effect as soon as the exciton pumping is important,
![]() . Cavity pumping becomes important again in a
system like 2, where it enhances significantly the output power, with
the price of superpoissonian statistics (
. Cavity pumping becomes important again in a
system like 2, where it enhances significantly the output power, with
the price of superpoissonian statistics (![]() ). With a poorer
system like point 3, some lasing effect can be found with the aid of
the cavity pump: there is a nonlinear increase of
). With a poorer
system like point 3, some lasing effect can be found with the aid of
the cavity pump: there is a nonlinear increase of ![]() and
and ![]() approaches 1 for
approaches 1 for
![]() . However, the weaker the coupling,
the weaker this effect until it disappears completely for decay rates
outside the range plotted in Fig. 5.13. In all
cases, the self-quenching leads finally to a thermal mixture of
photons (
. However, the weaker the coupling,
the weaker this effect until it disappears completely for decay rates
outside the range plotted in Fig. 5.13. In all
cases, the self-quenching leads finally to a thermal mixture of
photons (![]() ) and WC at large pumping.
) and WC at large pumping.
Elena del Valle ©2009-2010-2011-2012.


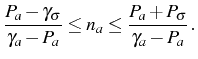
![\begin{multline}
g^{(2)}=\Big[g^2\big((n_a+1)(P_a^2+P_\sigma^2)-n_a(\gamma_a+...
...(4\Gamma_+^2+\Delta^2)\Big]\Big/2g^2n_a^2\Gamma_a\Gamma_\sigma\,.
\end{multline}](img1582.png)
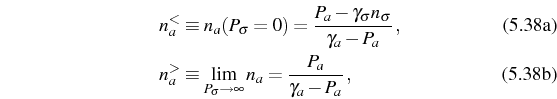
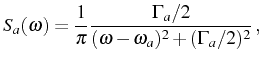
![$\displaystyle \frac{d\mathrm{p}[n]}{dt}=\gamma_a(n+1)\mathrm{p}[n+1]-\Big(\gamm...
...\mathrm{p}[n]+\frac{l_\mathrm{G}n}{1+l_\mathrm{S}/l_\mathrm{G}n}\mathrm{p}[n-1]$](img1606.png)