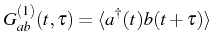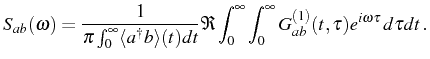First order coherence function and the power spectrum
Studying light-matter interaction in a given system, means probing the
Hamiltonian structure described in
Sec. 2.3. For that purpose, the ![]() manifolds need to be excited and the cavity mirrors must let particles
leak out so that we can measure them.
Emission (and excitation if it is incoherent) comes with the price of
decoherence. This decoherence changes the underlying manifold
structure (by broadening and renormalizing lines, in much the same way
as described by Weisskopf).
manifolds need to be excited and the cavity mirrors must let particles
leak out so that we can measure them.
Emission (and excitation if it is incoherent) comes with the price of
decoherence. This decoherence changes the underlying manifold
structure (by broadening and renormalizing lines, in much the same way
as described by Weisskopf).
In order to minimize the effects on decoherence and keep the SC physics as ``pure'' as possible, several experimental options are available, as explained for example by Agarwal & Puri (1986). The excitation can be of the kind of Eq. (2.68). In atomic physics, a coherent continuous wave (cw) pumping, in the form of a monochromatic laser shined on the atom, is used to probe (if weak) or drive (if strong) the system inside the cavity in the SS. In semiconductors, this excitation process corresponds to optical resonant excitation of the quantum dot or well. In this case, the direction of excitation and collection of the emission is the same. Exciting resonantly, it is difficult to distinguish the light emitted by the system from that reflected from the sample as they have similar frequencies. This is one reason why the experiments are usually done with nonresonant excitation. However, in the last few years, some experiments have been carried out where clever configurations allowed to resonantly drive a single self assembled QDs. Muller et al. (2007) used a waveguide as the excitation channel to separate it from the emitted light, reporting the first measurement of resonant fluorescence in this system.
A quantity that can be measured under the coherent cw, is the
amplitude of the field scattered by the driven atom,
![]() , given that the output is a coherent state of cavity
photons. The intensity of the scattered field
, given that the output is a coherent state of cavity
photons. The intensity of the scattered field
![]() is a function of the external
radiation frequency
is a function of the external
radiation frequency
![]() . If the laser intensity is
weak, the resonances of this function are related to the Rabi
frequency of the atom coupling with the cavity mode, renormalized by
dissipation, the only source of decoherence. Similarly, one can look
at the average rate of absorption of energy, the absorption
spectrum
. If the laser intensity is
weak, the resonances of this function are related to the Rabi
frequency of the atom coupling with the cavity mode, renormalized by
dissipation, the only source of decoherence. Similarly, one can look
at the average rate of absorption of energy, the absorption
spectrum
![]() , proportional to the atomic field
, proportional to the atomic field
![]() , or
, or
![]() depending on the matter model, with the
same resonances. With a weak probe, the spectral features of
depending on the matter model, with the
same resonances. With a weak probe, the spectral features of
![]() and
and
![]() can be similarly
found by assuming that the atom-photon system decays from a given
initial state without any driving source. This is even closer to the
experimental situation of pulse excitation as the result is to put the
system in a given state from which it decays. Instead of looking at
the SS imposed by the Hamiltonian in
Eq. (2.68), we will prefer to study the SE of
the system. This will allow us to compare our results of incoherent
pumping with the physics under coherent excitation, where the pump
does not play a role further than bringing particles.
can be similarly
found by assuming that the atom-photon system decays from a given
initial state without any driving source. This is even closer to the
experimental situation of pulse excitation as the result is to put the
system in a given state from which it decays. Instead of looking at
the SS imposed by the Hamiltonian in
Eq. (2.68), we will prefer to study the SE of
the system. This will allow us to compare our results of incoherent
pumping with the physics under coherent excitation, where the pump
does not play a role further than bringing particles.
Strong driving fields, such as those of Muller et al. (2007) provided by
resonant lasers, serve not only as the excitation source but also as
the coupling field that induces the Rabi oscillations. This method
allows to put more and more particles, going up the manifold ladder,
without adding any extra decoherence. There is a point where the
regime of the Mollow triplet, studied by Mollow (1969), is
entered. It consists in driving the 2LS into the very high manifolds
of excitations where
![]() . In this case, at resonance, the
two eigenenergies of the system [Eq. (2.62)]
in both manifolds are just
. In this case, at resonance, the
two eigenenergies of the system [Eq. (2.62)]
in both manifolds are just
![]() . The four
possible transitions correspond to only three frequencies
. The four
possible transitions correspond to only three frequencies
![]() and
and
![]() , giving rise to a triplet
resonance. This is an interesting configuration and we will come back
to it and its possibilities under incoherent excitation in
Chapter 5.
, giving rise to a triplet
resonance. This is an interesting configuration and we will come back
to it and its possibilities under incoherent excitation in
Chapter 5.
Finally, the case we will analyze in full depth is that of a SS driven by incoherent pumping. As we explained in the Introduction and the previous section, this is the most common way of exciting the system in semiconductor physics. We will look into how this kind of excitation can drastically modify the Hamiltonian manifold picture depending on the character of the particle, bosonic of fermionic. But, in the same way that dissipation allows for the investigation of the cavity output, incoherent excitation does not only hinder SC, it can also help them to emerge, depending on the configuration. We will compare our results with the SE from a general initial state for illustration of this and other points.
In the SS under incoherent exchange with the environment, quantities
such as
![]() or
or
![]() decay with combinations of
decay with combinations of
![]() and
and ![]() rates until they vanish. Therefore they cannot be
used to characterize the Rabi oscillations, completely washed out from
the averaged one-time quantities by the probabilistic uncertainty. The
most interesting and straightforward quantity to measure and study
them is the luminescence spectrum
rates until they vanish. Therefore they cannot be
used to characterize the Rabi oscillations, completely washed out from
the averaged one-time quantities by the probabilistic uncertainty. The
most interesting and straightforward quantity to measure and study
them is the luminescence spectrum ![]() . It is defined as
the mean number of
. It is defined as
the mean number of ![]() -particles in the system with frequency
-particles in the system with frequency ![]()
This is proportional to the intensity of particles emitted by the system at this frequency. It is convenient to define as well the normalized spectra
so that Eq. (2.75) is now the density of probability that a photon emitted by the system has frequency
After a change of variables,
at positive time delays
In the SS case, care must be taken with cancellation of infinities brought by the ever-increasing time
From the general Eq. (2.74) to the SS, Eq. (2.79), there is the cancellation of the diverging quantities by obtaining the final result as a limit of the time-integrated spectrum. The population and the correlator can be decomposed as a transient (TR) and steady-state (SS) values:
where
Substituting Eq. (2.80) in this expression, we can keep track of the terms that cancel (one can check a posteriori from the explicit results, the convergence of
Since the norm of the Fourier transform of
This discussion should motivate the physical meaning and validity of both formulas, and show the connections between them.
The first order cross correlation between two different field
(![]() and
and ![]() ),
),
produces the spectral counterpart of Eq. (2.78), the so-called cross correlation function:
This spectral function contains similar information than the power spectrum and can be also experimentally measured and analyzed, as has been argued by Karlovich & (2007).
Subsections Elena del Valle ©2009-2010-2011-2012.


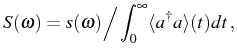
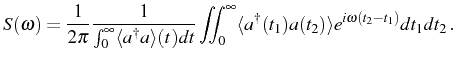
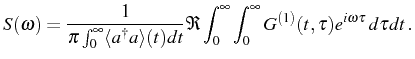
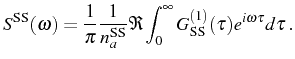
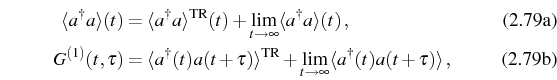
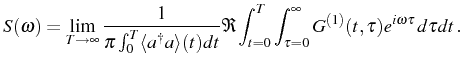
![$\displaystyle S^\mathrm{SS}(\omega)=\frac{1}{\pi}\lim_{T\rightarrow\infty}\frac...
...\rightarrow\infty}\langle\ud{a}(t)a(t+\tau)\rangle\bigg]e^{i\omega\tau}d\tau\,.$](img420.png)