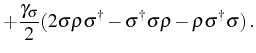Cavity QED (cQED)
Cavity QED (cQED) rests on the realization above that the lifetime of
an atom is not a property of the atom itself but of the coupled
atom-radiation field system. If one would be able to alter the
radiation field in some sense, such as for instance by suppressing its
fluctuations (including those of the vacuum!) or modifying its density
of states, this would alter the lifetime of an excited state, as
suggested by Eq. (1.1) if
![]() is
changed.
is
changed.
The effect was first put to use by Purcell (1946) in nuclear
magnetic resonance for the practical purpose of thermalizing spins at
radio frequencies, by bringing down their relaxation time
from
![]() s to a few minutes. Interestingly, this seminal
achievement in tailoring what was widely regarded before (since
Einstein's theory of spontaneous emission) as an intrinsic property of
matter, did not impress much Purcell himself or his contemporaries,
despite the good timing (Purcell did not attend the Shelter Island
conference, but Rabi, his then hierarchic superior, did). The effect
of tailoring lifetime through the density of optical modes is
nevertheless now known as the Purcell effect. Similar concepts
were investigated from a more fundamental angle by Casimir (1948),
for instance demonstrating the attraction between two conducting
plates close enough for--in the words of Casimir--``the zero
point pressure of electromagnetic waves'' being reduced between the
plates. With regard to SE, the problem was considered again for its
own sake by Kleppner (1981). In his initial proposal, he
considered it in the opposite sense than Purcell, namely, to increase
the lifetime of the excited state, by decoupling it from the optical
field (and therefore also from its vacuum fluctuations). Soon after,
Goy et al. (1983), from the Haroche group, reported the first
experimental observation of Purcell enhancement.1.8 The authors concluded their paper setting
the goal for a higher milestone of cavity QED: when spontaneous
emission is enhanced so much that absorption--which is equal to it
from Einstein's theory--or more specifically, since we have only one
emitter, reabsorption of the photon by its own emitter, becomes
dominant over the leakage of the photon out of the cavity, then the
perturbative--so-called Weak Coupling (WC)--regime breaks
down and instead Strong Coupling (SC) takes place. In this
case, emitted photons engage a whole sequence of absorptions and
emissions, known as Rabi oscillations, until their ultimate
decay out of the cavity. This regime is of greater interest, as it
gives rise to new quantum states of the light-matter coupled system,
sometimes referred to as dressed states (especially in atomic
physics) or as polaritons (especially in solid-state
physics). Experimentally, SC is more difficult to reach, as it
requires a fine control of the quantum coupling between the bare modes
and in particular to reduce as much as possible all the sources of
dissipation.
s to a few minutes. Interestingly, this seminal
achievement in tailoring what was widely regarded before (since
Einstein's theory of spontaneous emission) as an intrinsic property of
matter, did not impress much Purcell himself or his contemporaries,
despite the good timing (Purcell did not attend the Shelter Island
conference, but Rabi, his then hierarchic superior, did). The effect
of tailoring lifetime through the density of optical modes is
nevertheless now known as the Purcell effect. Similar concepts
were investigated from a more fundamental angle by Casimir (1948),
for instance demonstrating the attraction between two conducting
plates close enough for--in the words of Casimir--``the zero
point pressure of electromagnetic waves'' being reduced between the
plates. With regard to SE, the problem was considered again for its
own sake by Kleppner (1981). In his initial proposal, he
considered it in the opposite sense than Purcell, namely, to increase
the lifetime of the excited state, by decoupling it from the optical
field (and therefore also from its vacuum fluctuations). Soon after,
Goy et al. (1983), from the Haroche group, reported the first
experimental observation of Purcell enhancement.1.8 The authors concluded their paper setting
the goal for a higher milestone of cavity QED: when spontaneous
emission is enhanced so much that absorption--which is equal to it
from Einstein's theory--or more specifically, since we have only one
emitter, reabsorption of the photon by its own emitter, becomes
dominant over the leakage of the photon out of the cavity, then the
perturbative--so-called Weak Coupling (WC)--regime breaks
down and instead Strong Coupling (SC) takes place. In this
case, emitted photons engage a whole sequence of absorptions and
emissions, known as Rabi oscillations, until their ultimate
decay out of the cavity. This regime is of greater interest, as it
gives rise to new quantum states of the light-matter coupled system,
sometimes referred to as dressed states (especially in atomic
physics) or as polaritons (especially in solid-state
physics). Experimentally, SC is more difficult to reach, as it
requires a fine control of the quantum coupling between the bare modes
and in particular to reduce as much as possible all the sources of
dissipation.
Haroche's group in their first report of tuning the SE, placed this
higher goal only ``a tenfold increase in ![]() '' away. Shortly
after, they reported, with Kaluzny et al. (1983), the first observations
of Rabi oscillations. However, rather than increasing the
'' away. Shortly
after, they reported, with Kaluzny et al. (1983), the first observations
of Rabi oscillations. However, rather than increasing the ![]() , they
had used
, they
had used ![]() atoms, thereby enhancing the coupling strength by a
factor
atoms, thereby enhancing the coupling strength by a
factor ![]() . Unfortunately, my thesis does not explore in its
full generality the so-called Dicke Hamiltonian, that explains this
enhancement. However we shall see its manifestation in the particular
case of
. Unfortunately, my thesis does not explore in its
full generality the so-called Dicke Hamiltonian, that explains this
enhancement. However we shall see its manifestation in the particular
case of ![]() in Chapter 6. Haroche & Kleppner (1989) wrote an
authoritative review on the early cQED experimental
achievements.1.9
in Chapter 6. Haroche & Kleppner (1989) wrote an
authoritative review on the early cQED experimental
achievements.1.9
On the theoretical side, Sanchez-Mondragon et al. (1983) were the first to address the fundamental problem of the lineshape of the SE in cQED.1.10 They met with the difficulty of the definition of the optical spectrum, which had otherwise found an acceptable solution for physicists with the mathematical work of Wiener (1930) and Khinchin, even in the cases of non-stationary signals. But instead, under the guidance of Eberly, they had recourse to the more rigorous Eberly & Wodkiewicz (1977) time-dependent physical spectrum:
This expression is derived from physical (rather than mathematical) grounds, computing probabilities of measuring a photon by absorption from a detector, that introduces its linewidth
![\includegraphics[width=.5\linewidth]{introduction/sanchezmondragon-2.ps}](img65.png)
|
If only for reasons of self-consistency, cavity decay should be
included to describe any luminescence experiment, since photons should
leak out from the cavity to be detected, as duly noted by
Agarwal & Puri (1986), who added this ingredient ![]() (
(![]() in their notations) in a master equation for the coupled
light-matter system:
in their notations) in a master equation for the coupled
light-matter system:
![\includegraphics[width=\linewidth]{introduction/agarwal.ps}](img69.png)
|
The most complete quantum optical calculation, supported by the most insightful discussion, was brought by Carmichael et al. (1989), who considered the most general case with both types of decay:
(
![\includegraphics[width=.5\linewidth]{introduction/carmichael.ps}](img78.png)
|
In contrat with the two previous approaches, the PL spectrum was here computed with the formula:
which is the expression we shall later adopt in the case of time-dependent dynamics (case of SE) for several reasons. The main one is that the description of luminescence of the coupled light-matter system by Carmichael et al. (1989) is the most involved at this level of description and the one that, with Laussy et al. (2008b), I took as a starting point to formulate the counterpart of this problem for semiconductors. Another reason is that it frees us from the detector's linewidth, which does not need to enter the picture at a primary level, as it did in the two previous descriptions. It could be included in any case by the usual procedure of convolution. Finally, I will show later that formula (1.6) leads to the relevant case of the Wiener-Khinchin formula for the stationary fields.
Before closing this Section of the seminal experimental and
theoretical efforts in cQED that are the most relevant for our
subsequent discussion, I want to comment on the features that are
missing from Carmichael et al. (1989)'s description for my purposes, and
that I will provide in Chapter 3. Those are the
arbitrary initial condition (rather than merely the excited state of
the atom), and observation of the cavity emission (rather than only
the direct atom emission). The later case means computing
Eq. (1.6) with ![]() operators rather
than
operators rather
than ![]() , and should be an obvious requisite to the semiconductor
microcavity physicist. In their partial pictures, both
Sanchez-Mondragon et al. (1983) and Agarwal & Puri (1986) had addressed these
questions to some extent (but still far from full generality). The
former had considered various coherent states of the optical field,
and the latter had computed both the photon and exciton emission. I
want to comment quickly on the necessity of these extensions, though
we shall discuss them at greater length when I will address the
problem head on. It is clear that the initial condition strongly
influences the optical spectrum, as can be seen by considering as
initial states the excited state of the atom,
, and should be an obvious requisite to the semiconductor
microcavity physicist. In their partial pictures, both
Sanchez-Mondragon et al. (1983) and Agarwal & Puri (1986) had addressed these
questions to some extent (but still far from full generality). The
former had considered various coherent states of the optical field,
and the latter had computed both the photon and exciton emission. I
want to comment quickly on the necessity of these extensions, though
we shall discuss them at greater length when I will address the
problem head on. It is clear that the initial condition strongly
influences the optical spectrum, as can be seen by considering as
initial states the excited state of the atom, ![]() , or one
photon,
, or one
photon, ![]() on the one hand, and an eigenstate of the
Hamiltonian in Eq. (1.2),
on the one hand, and an eigenstate of the
Hamiltonian in Eq. (1.2),
![]() , on the other hand. These will normally (in
SC) produce, a two Rabi peaks and only one of them, respectively,
which are quantitatively very different. It is maybe less obvious that
, on the other hand. These will normally (in
SC) produce, a two Rabi peaks and only one of them, respectively,
which are quantitatively very different. It is maybe less obvious that
![]() and
and ![]() , also differ in their SE when
, also differ in their SE when
![]() , and in some case also
quantitatively. These considerations, that in this context might
appear as mere generalizations, will become a natural, and in fact,
compulsory, requirement in the semiconductor treatment, to which I now
turn.
, and in some case also
quantitatively. These considerations, that in this context might
appear as mere generalizations, will become a natural, and in fact,
compulsory, requirement in the semiconductor treatment, to which I now
turn.
Elena del Valle ©2009-2010-2011-2012.


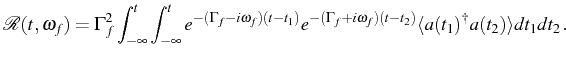
![$\displaystyle \partial_t\rho=-i[H,\rho]+\frac{\gamma_a}{2}(2a\rho\ud{a}-\ud{a}a\rho-\rho\ud{a}a)\,.$](img67.png)
![$\displaystyle \partial_t\rho=-i[H,\rho] +\frac{\gamma_a}{2}(2a\rho\ud{a}-\ud{a}a\rho-\rho\ud{a}a)$](img72.png)