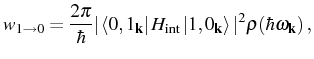Quantum Electrodynamics (QED)

Quantum Electrodynamics (QED) is the relativistic quantum field-theory that describes the interaction of light with matter.

It is the most successful theory ever conceived by man. The so-called fine structure constant $\alpha$ --the coupling strength of the interaction between electrons and photons--brings together some of the most important fundamental constants of physics:^1.1 $\alpha=e^2/(4\pi\epsilon_0\hbar c)$ . The numerical value of this constant embeds both the impressive achievements of science and its limitations. On the one hand, the theory has proven to be exact in predicting phenomena of light-matter couplings with an accuracy better than one part in a billion. On the other hand, there is no fundamental (or mathematical) explanation of its value, it has to be determined empirically. As a consequence, the best of our theories provides a very fine description of natural phenomena, but ultimately relying on what is essentially a fitting parameter.

The small value of the fine structure constant as compared to 1, $\alpha\approx1/137$ , allows to recourse to the techniques of perturbation theory, vividly expressed in terms of Feynman diagrams. QED is sometimes described as the perturbative theory of the electromagnetic quantum vacuum, and this is indeed this particular aspect that most books on that topic actually study. In this text, we shall contemplate a rather different angle at the same time as we focus on a very particular confine of the general theory, namely, to that which is known as quantum optics. It fits in the general picture as QED in the Coulomb gauge. We shall in particular discard relativity completely and rely on the Schrödinger equation (rather than Dirac equation), but we will, on the other hand, reach the nonperturbative regime of strong interactions, where quantum phenomena prevail and sweep away completely our classical intuition. Schrödinger immortalized his worries about one of the tenets of quantum theory--the principle of superposition--with his namesake cat that he imagined in a quantum superposition of alive and dead. Nowadays, there is no mysticism about the meaning nor doubt about the existence of such ``cat states''. One of the most important physical object that we will deal with throughout this text--the polariton--is specifically of this nature.^1.2 (We introduce it in next Section)

By studying the equilibrium properties of a gas of photons in a cavity, Einstein deduced the fundamental mechanisms of interactions of light with matter:

i: Spontaneous Emission (SE)
ii: Stimulated Emission

(Absorption is here regarded as a particular case of the stimulated process) The first mechanism refers to the return towards the ground (or an intermediate) state: when an atom has been excited and raised to an energy state higher than its ground state (with one electron having undergone a transition from its orbital to one of higher energy), it will ultimately recover its ground state by emitting a photon which carries away the energy of the transition. This decay of the excited state is spontaneous: it occurs randomly. Einstein derived and quantified it with the so-called coefficient.

The second mechanism seems more mysterious at first, it describes emission in presence of another photon: if the excited atom as above is in presence of a photon similar to one that would be emitted spontaneously (of about the same energy), then the atom decays towards its ground state emitting a clone photon of the original one, leaving two identical copies in the final state. Einstein quantified it with the coefficient.

and coefficients arise from Einstein's rate equations to fit the Planck distribution. They are still known as such nowadays.

The nature of the process comes from the Bose statistics, responsible for lasing and Bose-Einstein Condensation (BEC). Bose statistics itself follows from a requirement of symmetry of the wavefunction. In that respect, it arises naturally from elementary quantum mechanics (in the first quantization). The coefficient thus comes straightforwardly from perturbation theory, with the original photon playing the role of the perturbative field.

The origin of the coefficient cannot be traced at the same level as that of its counterpart: an excited state without any perturbation acting on it should remain as it is, according to Schrödinger equation that forbids explicitly spontaneous (or nondeterministic) events of the like of SE.^1.3 Already in the so-called ``old quantum theory'', it was felt by Bohr that SE was of a curious origin: the atom makes a quantum jump which is probabilistic and without a cause. Of course, phenomenologically, one can introduce a decay rate, and this is the procedure Einstein used to fit the observed data. In this sense the temptation is great to think of this decay as an intrinsic property of the atom, its lifetime. Dirac (1927) was the first to study the microscopic origin of the coefficient, in the framework of the quantum theory of radiation, soon known as QED (he was the first to use that term). Dirac's extension of Schrödinger equation to include relativity still found, remarkably, an exact solution to the problem of the hydrogen atom, providing a complete, exact and self-contained picture of special relativity and quantum mechanics working together. One consequence of this theory was that states with the same and but different quantum numbers are degenerate. In a cleverly set up experiment to challenge this prediction, Lamb Jr. (1947) evidenced the contrary with what is now known as the Lamb shift, between the states $2s_{1/2}$ ( ) and $2p_{1/2}$ ( ). This showed that even a relativistic quantum description of the hydrogen atom was not, after all, complete! This caused a great turmoil at the time, specifically during the first Shelter Island Conference on the Foundations of Quantum Mechanics in 1947. Bethe (1947) quickly worked out a non-relativistic argument involving vacuum fluctuations that showed how a good numerical estimate could be obtained. In this attempt, he had to deal more directly than ever before with the famous problem of divergences that plague Dirac's quantum theory of radiation, the resolution of which--initiated at the Shelter Island conference that also attended Schwinger and Feynman--led to the full-fledged QED.

Back to the late 20s, Weisskopf, then a student in Göttingen, addressed the problem of the emission of one excited state to a stable (ground) state. He did not encounter divergences^1.4 as he neglected most of the relativistic features but his treatment was nevertheless directly inspired by Dirac's treatment of the radiation field. Franck proposed Weisskopf to investigate the case of transitions between two excited states, that, however, he could not solve by himself (he once said that if he had had the proper mathematical training, he would have calculated the Lamb shift even before it was found). He put the question to a visiting Wigner who worked it out with him on the spot. Agreeably surprised by the outcome, Weisskopf & (1930) wrote a joint paper, now famous.^1.5 The outcome that pleased them both was the way the final linewidth built up from broadenings of the various states involved in the transition. The problem does not occur when the transition is from an excited state to the ground-state, which is not broadened. This is this case that the young Weisskopf solved by himself, and which is the one most frequently reported as Weisskopf-Wigner theory (sometimes with more than was there in the first place, like calculation of the Lamb shift). Interestingly, we shall see in my formulation of the problem that the Weisskopf-Wigner concerns revive in my treatment that includes the excitation, because, with an incoherent pumping term--such as the one that I will introduce--the ground state gets broadened too, and this bears some interesting consequences on the problem. But rather than considering any source of excitation, Weisskopf and Wigner considered the SE of the initial state $\ket{1,0_\mathbf{k}}$ , where the atom is in its excited states and all modes of a continuous radiation field are devoid of photons.^1.6 They computed with the Dirac equation (that is in fact the Schrödinger equation in their approximations) the time evolution of the amplitude for $\ket{1,0_\mathbf{k}}$ and states $\ket{0,1_\mathbf{k}}$ for the various $\mathbf{k}$ that could have received the emitted photon. Even in this simplified picture, the problem is short of trivial. For our analysis it is enough to consider their result in the form of the Fermi's golden rule, which is an approximation for the rate of transition from the initial state to the bulk of photon modes:

$\displaystyle w_{1\rightarrow0}=\frac{2\pi}{\hbar}\vert\bra{0,1_\mathbf{k}}H_\mathrm{int}\ket{1,0_\mathbf{k}}\vert^2\rho(\hbar\omega_\mathbf{k})\,,$

(1.1)

where $H_\mathrm{int}$ is the light-matter coupling $\mathbf{\mu}\cdot\mathbf{E}$ and $\rho(\hbar\omega_\mathbf{k})$ the density of optical modes. The main value of Weisskopf-Wigner approach, at least in their view, was an alternative microscopic derivation of the mechanism of the exponential SE in quantum theory, with the same rate that had been given previously by Dirac, Eq. (1.1). Although the Schrödinger equation is reversible, the Weisskopf-Wigner model devised an insightful mechanism--with a coupling of a single mode (the excited atom) to a continuum (the empty radiation field)--where irreversibility emerges from a Hamiltonian (cyclic) dynamics. This mechanism is the first step towards the modern description of decay in terms of coupling to external reservoirs, a formalism that I will review briefly in Chapter. 2.

The modern QED picture accounts for the Lamb shift, with the accuracy evoked previously, by summing-up various contributions (various Feynman diagrams) of opposite tendencies (like the anomalous magnetic moment, and the vacuum polarization). But the most important effect is the one captured by Weisskopf and Wigner's mechanism and advanced by Bethe, that of the renormalization of the electron mass by its interaction with the electromagnetic field (in vacuum). This was further studied by Welton (1948), who also suggested that fluctuations of the vacuum were responsible for spontaneous emission. In Dirac's interpretation, this was attributed to QED radiation reaction, but, as was later realized by Milonni et al. (1973), this is essentially the same with some reordering of operators.

Another important name of the field, Jaynes, was also thinking in terms of back-action of the electromagnetic field on the atom, but with the view that quantization of the field was not necessary, at least not to explain the Lamb shift, SE or any related phenomena. He accepted the challenge to demonstrate the Lamb shift from these grounds (without photon field quantization) in within 10 years! He could indeed reproduce, with great efforts from himself and his students, the result qualitatively, but he failed to match the same accuracy that QED was providing so elegantly.^1.7Ironically, the model Jaynes & Cummings (1963) developed as a support of Jaynes' so-called neoclassical theory, against field quantization, is now the most famous example of quantum optics and cQED. The celebrated Jaynes-Cummings (JC) model provides the fundamental picture of light-matter interactions at the ultimate quantum level: when only one mode of light (an harmonic oscillator, HO) is interacting with only one mode of matter $\sigma$ (a two-level system, 2LS), and single quanta are mediating the interactions. Its Hamiltonian reads:

$\displaystyle H=\omega_a\ud{a}a+\omega_\sigma\ud{\sigma}\sigma+g(\ud{a}\sigma+a\ud{\sigma})\,.$

(1.2)

Here, $\omega_{a,\sigma}$ are the free energies for the modes and

is their coupling strength. The physics of this system is to be investigated in specially prepared conditions, where these single modes have been properly selected and isolated. This is the topic of next Section.