Correlated Photon Dynamics in Dissipative Rydberg Media. E. Zeuthen, M. J. Gullans, M. F. Maghrebi and A. V. Gorshkov in Phys. Rev. Lett. 119:043602 (2017). What the paper says!?
This relates to our liquefaction of light:
«We then show how this system can generate a regular train of single photons from uniform coherent-state input.»
This covers CW driving, as opposed to other works that focus on pulsed excitation. Its transformation of light is more interesting than the usual photon blockade:
«At a more fundamental level, the emergence of a strongly correlated state of photons from a classical input is an interesting case study for emergent behavior in nonequilibrium quantum many-body systems.»
In our case, not only the input is classical, it is also incoherent, and there is no many-body physics involved.
They model the process with hard spheres, which makes it even closer to us:
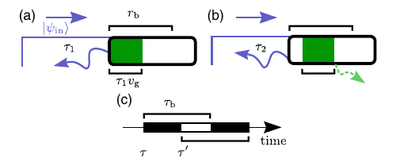
It is not too clear to me why the first photon gets scattered while still creating a polariton (they call that "projection of the wavefunction") and I would have sketched more than one rod in (c), but the main thing is that they indeed root their description into the hard sphere model. As a result, basic results directly correspond to ours, e.g., their Eq. (2) and [1]'s Eq. (3). More notably, they compute the first-order correlation function in a form familiar to Sana's $g^{(2)}$:
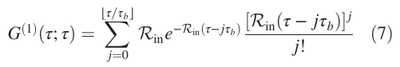
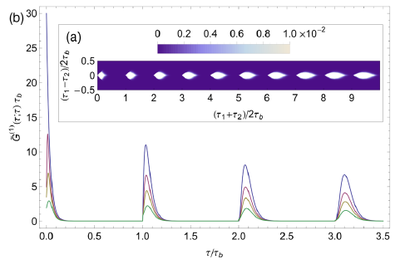
The scheme appears complicated and fragile, though:

They make a reference, but quite obscure, to Wilczek's time crystal:
«to turn the photon trains into time crystals that keep their periodicity for times that are exponentially long in the input intensity.»
The work is used (and explained, cf. Sec. IIA) in Ref. [2]
References
- ↑ Perfect single-photon sources. S. Khalid and F. P. Laussy in Sci. Rep. 14:2684 (2024).

- ↑ Photon propagation through dissipative Rydberg media at large input rates. P. Bienias, J. Douglas, A. Paris-Mandoki, P. Titum, I. Mirgorodskiy, C. Tresp, E. Zeuthen, M. J. Gullans, M. Manzoni, S. Hofferberth, D. Chang and A. V. Gorshkov in Phys. Rev. Res. 2:033049 (2020).