Photon propagation through dissipative Rydberg media at large input rates. P. Bienias, J. Douglas, A. Paris-Mandoki, P. Titum, I. Mirgorodskiy, C. Tresp, E. Zeuthen, M. J. Gullans, M. Manzoni, S. Hofferberth, D. Chang and A. V. Gorshkov in Phys. Rev. Res. 2:033049 (2020).  What the paper says!?

The paper was pointed out to me by one of its Authors (3rd one) following discussions of our liquid light in Mexico city at the Etic Tlahuilli school. It indeed discusses the "unconventional shapes of measured correlation functions". This led me, through its references, to the series of papers that study the two-correlation function of our perfect single-photon source, in particular:

1. Attractive photons in a quantum nonlinear medium. O. Firstenberg, T. Peyronel, Q.-Y Liang, A. V. Gorshkov, M. D. Lukin and V. Vuleti\'c in Nature 502:71 (2013).
2. Wigner Crystallization of Single Photons in Cold Rydberg Ensembles. J. Otterbach, M. Moos, D. Muth and M. Fleischhauer in Phys. Rev. Lett. 111:113001 (2013).
3. Many-body physics of Rydberg dark-state polaritons in the strongly interacting regime. M. Moos, M. Höning, R. Unanyan and M. Fleischhauer in Phys. Rev. A 92:053846 (2015).
4. Correlated Photon Dynamics in Dissipative Rydberg Media. E. Zeuthen, M. J. Gullans, M. F. Maghrebi and A. V. Gorshkov in Phys. Rev. Lett. 119:043602 (2017).
5. Observation of three-photon bound states in a quantum nonlinear medium. Q. Liang, A. V. Venkatramani, S. H. Cantu, T. L. Nicholson, M. J. Gullans, A. V. Gorshkov, J. D. Thompson, C. Chin, M. D. Lukin and V. Vuletić in Science 359:783 (2018).

These papers overall study the Rydberg blockade mechanism, whereby propagation of light under condition of electromagnetically induced transparency. The "natural next step" of "the realization of a regular train of single photons" is explicitly mentioned

This one, specifically, focuses on an accurate description, based on a 'hard-sphere serialized model' and the more accurate matrix product states formalism, of the i) shape of the pulse emitted by the gas and ii) its $g^{(2)}$, to best match experiments (that are performed). There is less good agreement at high photon flux, which the Authors attribute to "pollutants" (Rydberg atoms that remain excited and disrupt the process).

They expand on Zeuthen et al. by considering arbitrary pulse shapes as opposed to CW, focusing in particular on the Tukey type, i.e., flat top. They also, to some extent, consider CW in the flat region of the pulse, although at higher pumping, the emission decays in time (Fig. 4d).

They describe oscillations of the time ordering as "humps", whose physics is perceived as a complex interplay of various factors:

This is Fig. 1(d) and the caption describing the "humps" (this time plural):

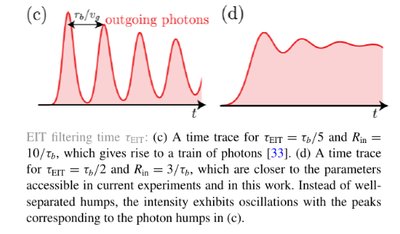
A hump is produced at the arrival of the pulse, and is also expected at its termination. Only the arrival-hump is observed experimentally, which is attributed to pollutants.

They measure $g^{(2)}$ in the stationary region and observe the growth of the hump at pumping is increased:

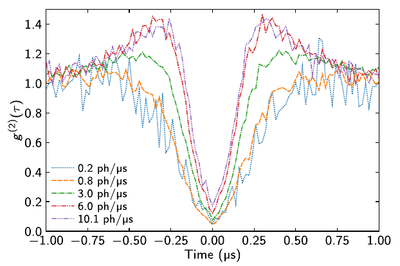
A major contribution of this work is indeed the various limitations of Rydberg blockade due to pollutants:

The likely scenario is sketched in Fig. 8. An effective pollutant model is developped.