Quantifying the Coherence between Coherent States. K. C. Tan, T. Volkoff, H. Kwon and H. Jeong in Phys. Rev. Lett. 119:190405 (2017).  What the paper says!?

The Authors introduce a resource theory of linear optics, recognizing that "coherence" as defined in the former is very different from "coherence" as understood in quantum optics:

The approach they criticize is that which regards the "classical" or "incoherent" states as the Fock states $\ket{n}$, which is however and indeed not a correct picture for light.

Specifically, they introduce the $\alpha$ coherence, which is the particular case for coherent state $\ket{\alpha}$ of their extension of the resource theory for finite-dimensional Hilbert space introduced by Baumgratz  et al. This identifies the "incoherent" (or resource) states as those which are nonclassical in the quantum optical sense (negative $P$ distribution).

In this Letter, we propose an approach which demonstrates that the quantum resource identified by Baumgratz, Cramer, and Plenio [10] is essentially the same as the notion of nonclassicality identified by Glauber [27]

There is an irritating difficulty in figuring out which coherence the Authors refer to:

• coherence resource = nonclassicality in quantum optics (abstract)
• incoherent states I (resourceless or classical) are the coherent states (quantum optics)

The Authors make a poor job in avoiding such conclusions. For instance, they define incoherent states (resourceless or classical) as those which are diagonal in a basis of incoherent states:

And a few lines below, they say that every quantum state is diagonal in the basis of $\ket{\alpha}$:

Since those are the incoherent states, this seems to say that all states are incoherent. They imply here that $P$ must be positive for the "diagonal" criterion to apply.

The definition of the $\alpha$-coherence is not very clear and is apparently also difficult to compute in practice:

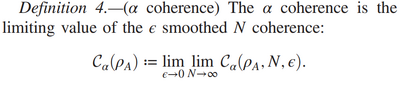
The ε-smoothed version is a (set-)topological one computing over all states in a ball centered on the quantum state.

To make things worst, I believe there is a typo in this statement:

the α coherence, is shown to identify incoherent states with nonclassical states in the sense of the Glauber-Sudarshan P distribution

The underline (mine) should read "non-incoherent", rather than "coherent" as the incoherent states (in resource theory) are precisely the coherent states (in quantum optics). This shows how broken is the whole terminology in this business.

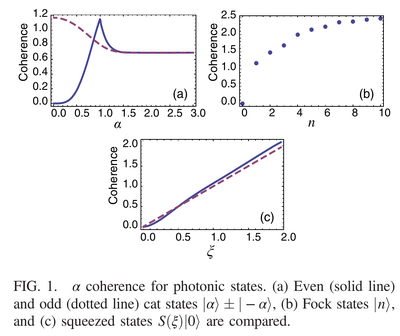
The results are, however, more clear: