«all the results for quantifying the quantum coherence assumed the finite-dimensional setting, which is neither necessary nor desirable.»
Quantifying coherence in infinite-dimensional systems. Y. Zhang, L. Shao, Y. Li and H. Fan in Phys. Rev. A 93:012334 (2016). What the paper says!?

This brings quantum resource theory to infinite-dimensional Hilbert spaces, in particular, quantum-optical spaces of photons. This seems to be one of the earliest efforts to do so. This is a pretty straightforward extension of the finite-space case[1]—in particular, also using the relative entropy of coherence as a measure of coherence—to which they add an energy constraint:
They limit to the relative entropy of coherence as the $l_1$ norm of coherence fails in infinite dimensions (detailed in Section IV, where it is, however, shown to work if also fluctuations are required to be finite, which seems reasonable):

It takes the view that coherent states are strongly quantum-mechanical:
The laser [2] and superfluidity [3] are two famous examples of quantum coherence, whose effects are evident at the macroscopic scale.
As a result, the coherent state $\ket{\alpha}$ has quantum coherence (as a resource), although it is not the most coherent one. The maximal-coherent state is the pure state with thermal distribution:
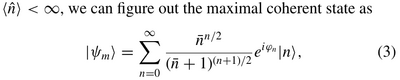
The incoherent states are, on the other hand, states which are diagonal in the Fock basis. So a Fock state is incoherent in this picture!

The thermal state, however, has no quantum coherence (as could be expected).
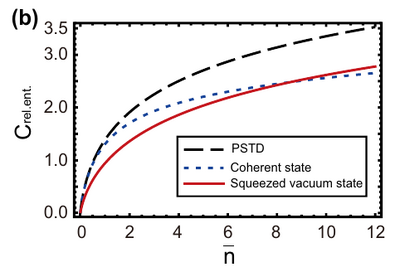
On the important—maybe the most important—question on how such quantum coherence can be converted into something genuinely and clearly useful, such as entanglement, they overview this very rapidly without introducing notations:

From this, it would appear one can extract entanglement from the coherent state, but this follows from using the ancilla as a Fock state, apparently (so not really incoherent in the first place). The infinite dimension of the ancilla space is unclear. This seems to be bogus logic here.
They then extend their results to the multimode case, finding it even better:
increasing the number of modes of light can enhance the coherence as a resource in quantum information processing.
Although in this case too, two-mode coherent states (thus with no correlations) also exhibit very strong "quantum coherence" (which is magnified when passing through a beam-splitter, although it does not give rise to entanglement).