«quantifying quantum coherence are implicitly assuming a finite-dimensional setting, which is neither necessary nor desirable.»
Quantifying coherence of Gaussian states. J. Xu in Phys. Rev. A 93:032111 (2016). What the paper says!?

This follows up from Ref. [1] which they criticize as not providing closed-form expressions in the type expected for Gaussian states:

In particular, like them, they define the incoherent states as the Fock states, and states diagonal in this basis:
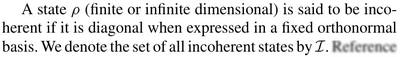
They then focus on Gaussian states, and arrive to the conclusion that all Gaussian states (except thermal states) are coherent.
This is because, they show that ««the diagonal one-mode Gaussian states are just thermal states»»:

Another interesting result is that maximally coherent states (as understood in this work) are pure states.
They also discuss other aspects such as operations that preserve coherence, finding that it must map thermal states into thermal states, and also the multimode case.
They leave various open questions, but particularly:
how do we quantify the coherence of physically relevant non-Gaussian states? [and] how about the behaviors of coherence in Gaussian dynamical systems, such as the phenomenon of frozen coherence?
The first question shows that the approach is too limited for quantum-optical concerns.