Semiconductor Quantum Dot: A Quantum Light Source of Multicolor Photons with Tunable Statistic. D. V. Regelman, U. Mizrahi, D. Gershoni, E. Ehrenfreund, W. V. Schoenfeld and P. M. Petroff in Phys. Rev. Lett. 87:257401 (2001).  What the paper says!?

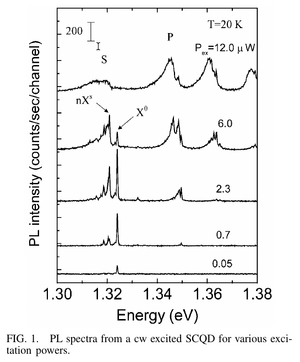
Auto- and cross-correlations in a multiexcitonic quantum dot cascade are studied (they say they have «measured for the first time temporal correlations between photons of different colors»). At low power, only the exciton ($X^0$) is observed, and it is antibunched. Increasing power, new lines $nX^s$ are reported and cross-correlated to the exciton.

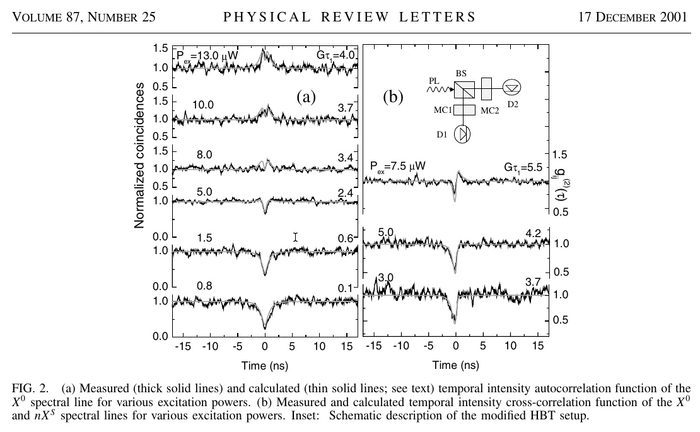
This gives a very beautiful characterization neatly summarized in their Fig. 2:

They use rate equations from previous papers. Specifically here, they solve:

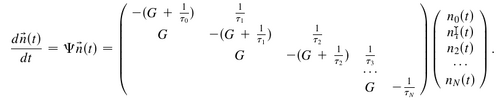
They find the steady-state exactly and the formal form of the transients:

This allows them to compute $g^{(2)}$ from the population conditioned to its initial condition. They say that they solve the equation analytically, although they don't give details or explicit results:

There, $n_j^i(\tau)$ seems to be the solution for the $j$th probability conditioned on the $i$th one. The validity of this procedure is a bit unclear.

$n_0(t)$ is the probability for the QD to be empty. $G$ is the pumping rate which they call "the cw e-h pairs photogeneration rate." Importantly, it links all successive steps in the cascade. $\tau_i$ are the $i$th multiexciton decay times, so that although it appears in the equation (for symmetry and/or elegance), $\tau_0=\infty$.

They provide the famous (Carmichael) solution for $N=1$:

On the asymmetry of the cascade:

A Mathematica Monte Carlo code can easily simulate their case: RegelmanCascade.nb.