Mollow triplet
The Mollow triplet—named after Benjamin Mollow who first provided the exact result, at and out of resonance—is the lineshape of a two-level system under a strong driving field.[1] It represents the high-driving regime of resonance fluorescence and is also known as the dynamic [or AC] Stark effect, itself also known as the Autler-Townes effect[2]). This is one of our favourite scientific objects, being a treasure trove of multiphoton correlations.
The name comes as a deserved tribute to Mollow's first exact as well as insightful derivation of the correct lineshape. This was no little achievement if one considers the considerable amount of controversy that surrounded the nature of the emission:
disagreement has been considerable and even extends to such gross features as the general shape of the spectrum.
— Carmichael & Walls[3]
The paper itself is a gift from at least providence, published on Christmas 1969 on page also 1969, and the first one of volume 188:[1]

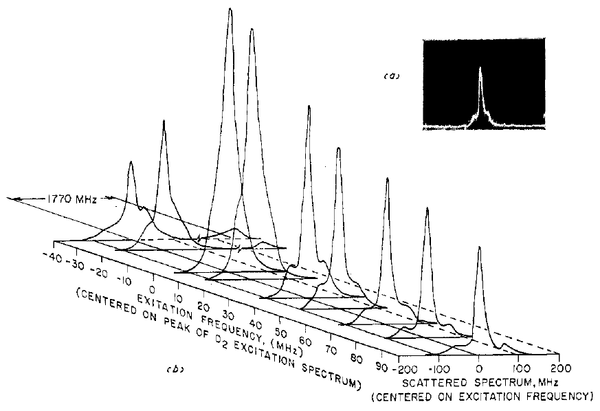
Its first experimental observation was made by Schuda et al.[4] in sodium vapour (although, at resonance, their "triplet" is not fully split even at their highest power).
The second Author, Carlos Stroud Jr., was a theorist who had a fully-quantized version for the lineshape (as opposed to Mollow's semiclassical one), and one can read some opposition to semiclassical models, although those of optical nutation, not that of Mollow (who is just cited without further comments). This passage is particularly interesting:
Because of the importance of spontaneous emission in this problem, some of the theoretical attempts to predict the spectrum have used quantum electrodynamics (Stroud 1973). Unfortunately, because of the difficulty of the QED calculations, they have been carried out only for the initial transient regime; the long term solutions are unknown. There may or may not be a ‘saturation steady-state limit’ as in semiclassical theory (Brewer and Shoemaker 1973). The results of these calculations predict a spectrum qualitatively similar to that measured above but differing in some respects. In particular the predicted ratio of the heights of the central peak to the sidebands is 2:l at resonance (Stroud 1973). Secondly, the areas under the side-bands are predicted to differ from each other appreciably for the detunings studied, whereas experimentally they appeared nearly equal when the laser was tuned to the high frequency side of the transition.
While Stroud's result received some support, even when including multiphoton processes[5], it was clarified by Hassan and Bullough[6] that the semiclassical approximation is however correct and that the problem was with a one-photon approximation.
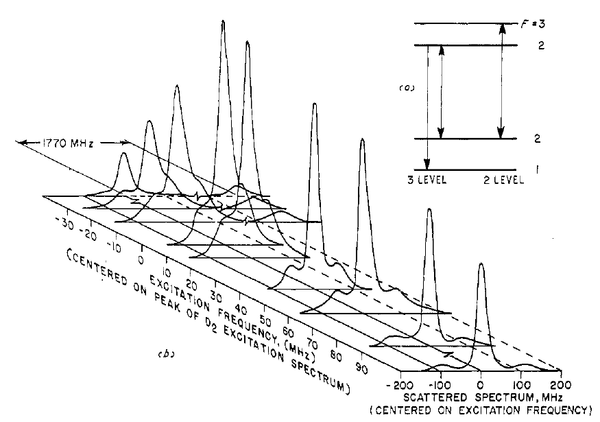
Schuda's setup was refined by Walthers and friends (R. Schieder, W. Hartig and V. Wilke)[7] still on sodium but on a different transition to yield these Mollow triplets (this time with a splitting at resonance):
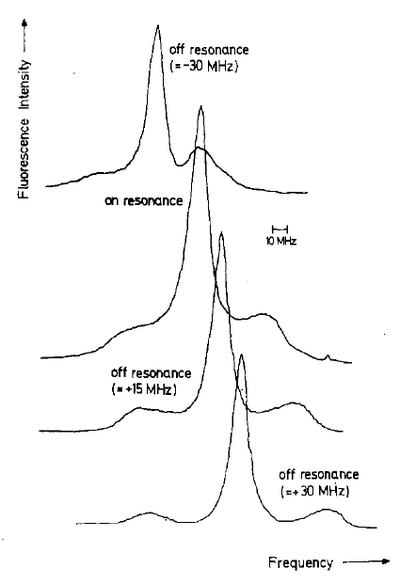
Mollow triplets are nowadays resolved with splendid resolution. See also a gallery of Mollow triplets.
Mollow's result was still challenged in 1975[8].
The shape is mesmerizing:
The curious feature of the spectrum is that neither the widths nor the heights of the side peaks are the same as that of the central peak.
— J. H. Eberly, [9]
An interesting account is by Mollow himself in the XIXth volume of Emil Wolf's Progress of Optics.[10]
Descriptions
Here are how various people have described the process:
The appearance of the Mollow triplet can be understood as the result of the periodic modulation of the density matrix elements and thus the molecular polarization at the Rabi frequency.
References
- ↑ 1.0 1.1 Power Spectrum of Light Scattered by Two-Level Systems. B. R. Mollow in Phys. Rev. 188:1969 (1969).
- ↑ Stark Effect in Rapidly Varying Fields. S. H. Autler and C. H. Townes in Phys. Rev. 100:703 (1955).
- ↑ A comment on the quantum treatment of spontaneous emission from a strongly driven two-level atom. H. J. Carmichael and D. F. Walls in J. Phys. B.: At. Mol. Phys. 8:L77 (1975).
- ↑ Observation of the resonant Stark effect at optical frequencies. F. Schuda, C. R. Stroud Jr and M. Hercher in J. Phys. B.: At. Mol. Phys. 7:L198 (1974).
- ↑ QED calculation of the resonant Stark effect. M. E. Smithers and H. S. Freedhoff in J. Phys. B.: At. Mol. Phys. 7:L432 (1974).
- ↑ Theory of the dynamical Stark effect. S. S. Hassan and R. K. Bullough in J. Phys. B.: At. Mol. Phys. 8:L147 (1975).
- ↑ Atomic fluorescence induced by monochromatic excitation. H. Walther in Proceedings of the Second Laser Spectroscopy Conference, Megève, France (1975).
- ↑ Multiple spontaneous emissions and interference effects in resonance fluorescence. S. Swain in J. Opt. B 8:L437 (1975).
- ↑ Atomic Relaxation in the Presence of Intense Partially Coherent Radiation Fields. J. H. Eberly in Phys. Rev. Lett. 37: (1976).
- ↑ Progress in Optics. B. R. Mollow in Theory of intensity dependent resonance light scattering and resonance fluorescence vol°XIX (1981).