«can [one] really speak about a nonequilibrium BEC of polaritons or whether one has just realized another exciton laser.»

Coherence of condensed microcavity polaritons calculated within Boltzmann-Master equations. T. D. Doan, H. Thien Cao, D. B. Tran Thoai and H. Haug in Phys. Rev. B 78:205306 (2008).  What the paper says!?

In this paper, the Authors describe ODLRO and two-photon coherence of polariton BEC, going beyond Boltzmann equations. They find neat quantitative agreement for $g^{(1)}$ but not that good for $g^{(2)}$, although qualitatively the transition from thermal to coherent is captured. In the first part, the address the question

to which extent the observation of the spatial coherence [...] can be explained in terms of a semiclassical Boltzmann ki-

netics

and come to the conclusion that:

one can calculate directly the spatial variation in the first-order coherence function and its dependence on the pump power by using the distributions obtained from the

Boltzmann kinetics.

They compute «the first-order spatial coherence function defined as»

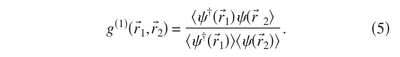
which they claim depends on the populations only ($b$ are the polariton operators):

This is, they say, «in the free-particle approximation», which is valid for Boltzmann equations but not for their later quantum extensions with which, by the way, they do not compute such quantities!

Their polariton-polariton Hamiltonian is (it is confusingly written, since $\vec{q}$ for instance is not defined):

They also show that their approach can deplete the condensate:

We include gain saturation and interactions

which deplete the condensate

They criticize Sarchi & Savona's strong depletion of the condensate since their dynamics «give the observed off-diagonal spatial coherence, which leaves not much space to larger depletion effects.» Their calculations indeed agree well with Deng et al.'s power dependence of $g^{(1)}(\Delta r)$ for fixed~$\Delta r$ (which they reproduce as Fig. 2). A better quantity, more difficult to obtain experimentally for large distances, is as a function of $\Delta r$, where, this time, they «see a more or less exponential decay of the coherence function»:

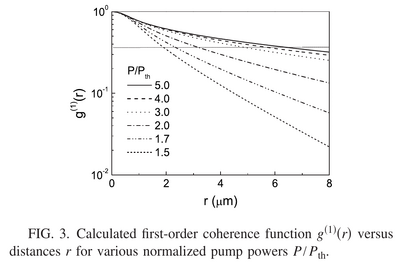
as indeed was observed experimentally (their Fig. (4)).

Then they turn to $g^{(2)}$ and how this varies with pumping, referring to experiments. To compute it, they mention four possibilities:

1. Langevin equations (used previously by Haug)
2. Some Associate Fokker-Planck equation (unclear what this is, exactly, see their Ref. [14])
3. My approach based on the Boltzmann quantum master equations, which is the one they adopt.
4. Schwendimann and Quattropani who include $g^{(2)}$ in the kinetic equations.

This is how they describe my work:

The Yamamoto experiment shows a slow decay of $g^{(2)}$ from less than 2 to more than 1. The QBME, on the other hand, predicts a fairly swift transition from 2 to 1, accompanying the condensation.

They call $W_{n_0}(t)$ what we call $p_{n_0}(t)$ the probability to have $n_0$ particles in the ground state:

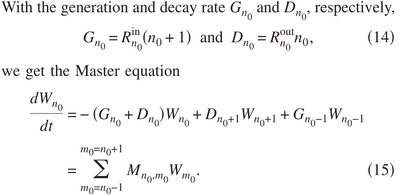
The key point is that the rates now depend on $n_0$ a random variable as opposed to, previously, a mean value (so, really, $\langle n_0\rangle$).

The distributions they find as a function of pumping look like this:

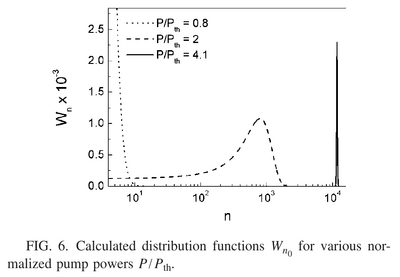
We see how the thermal limit with $g^{(2)}$ = 2 and the coherent limit with $g^{(2)}$ = 1 are smoothly connected. The

transition takes place in the region of pump powers $P\approx2P_\mathrm{th}$.

But this is much more abrupt and a stonger effect than observed experiments, so they conclude:

It seems that other many-body effects have to be included in order to account for the differ-

ence between these experimental findings and the theory.

They include polariton-polariton interactions from Schwendimann & Quatropanni which require Lorentzian instead of Dirac $\delta$ since these don't conserve energy. This also breaks detailed balance. That provides them with a counterpart of my phonon-induced QBME to include polariton-polariton relaxation:

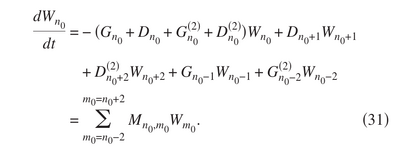
They also «incorporate the saturation effect kinetically in the Master equation» (exciton bleaching and Mott transition), in Sec. VB.

They solve the master equation iteratively:

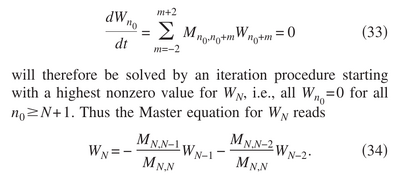
They obtain results (with, Fig. 10 or without, Fig. 9 below, saturation by exciton ionization) that they say match better with the experiment, but this is unclear, as they still observe a steep decrease but with an "oscillation" in the transition.

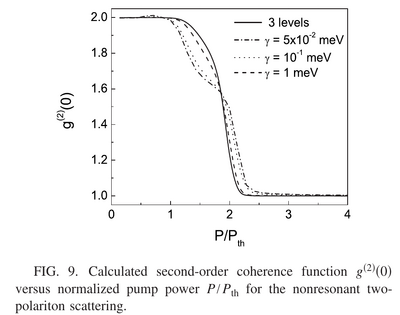
It's not quite clear what $\gamma$ is here, apparently the parameter in their Eq. (28).

They say that Sarchi et al. is similar to their approach.

They make an approximation from Eq. (10) to (13) which is not explained or justified, although they linked them with a "thus" on unrelated processes which do not alter the populations.

There is some discussion on what defines the size of the system (spot size vs sample size).