Exciting something with light is such a basic notion, it does not even have a proper subject classification. You would call that "optical excitation", for instance, but it's not something for which you would find a page on Wikipedia. Depending on whom you ask, the closest match could turn out to be something quite different. I would intuitively think of "spectroscopy", which however by far neither fully includes nor is fully included in the original concept.
The modern equivalent of humankind mastering fire is certainly our mastering of the laser. There, "exciting something with light" really became something! Applications are countless, from medical ones (eye-surgery, dermatology, cancer treatment, dentistry, etc.) to technology (especially for communication; think CDs, bar-code scanners, laser pointers and fiber-optics), passing by extremely delicate operations such as laser cooling, nuclear fusion, etc., or at the other end of the spectrum, more brutal things like welding and cutting, drilling holes, soldering, aligning tiles, etc., Even actual weapons, and I don't mean here as an optical guide, but an explicit high-power laser, something known as a DEW, of which you can read, in bemusement, among other "advantages" of the device: evading an accurately aimed laser after it has been fired is impossible. And I'm leaving loads apart, including some I would have like to keep as neat illustrations (would you have remembered the laser harp, for instance?) There is a list of laser applications on Wikipedia. And new stuff continuously keeps popping out. I was reading in National Geographic when coming back from the BuildMoNa symposium that now we look for entire pre-Colombian cities in South-America with so-called lidars, that go radar with a laser. Definitely, the laser is the modern's man grasp on the torch.
Something that interests me as a working scientist is molding quantum states of light with a laser. The basic idea is indeed very basic: you excite a quantum system with a laser:
Here I sketched the quantum system as a little pyramid, thinking of a self-assembled quantum dot. If we look closer at the light of the laser (red) and the one produced by the quantum system under this laser excitation (blue), we see that we turned in this way our laser light into quantum light, which I sketch here by explicitly drawing photons, that become the relevant particle objects to describe light, rather than, before, a wave, when photons were all merrily passing by with no correlation with their neighbors. By using other types of quantum systems, more complicated or with some tweaking and engineering, you can make your photons behave differently.
Anyway, at this point, one might ask a natural question: how about using this light where photons are now more prominent to excite something else?
Exciting with quantum light...
How about that? Now that's again such a basic notion—albeit one for a reduced set of people in the business of quantizing things—that it too is difficult to classify as part of a discipline, topic or even concept, even though a lot of works tackle this problem in some way and to some extent.
Well, we decided to address this question in the light of our other signature result: the theory of frequency correlations. This allows us to unravel the structure of photon correlations from any given optical source, and even brought us to discover a particular family of processes, that we called "leapfrog processes", which are the carrier of the quantum features of an emitter. With this knowledge, one can excite a target not with all the light taken indiscriminately from the emitter, but filtering it to distillate the quantum juice out of it. Therefore, we decided to address the problem of exciting with quantum light full-front and fully. This led us to a recent publication, Exciting polaritons with quantum light by López Carreño et al., PRL (2015).
"Ah-ah", I hear you say, "already you're speaking of something else! What are polaritons doing in here?"
I'll really speak of Exciting with quantum light (without polaritons) in the following. The fact they appear in our first output on that topic is that the problem is so large with so many ramifications, we couldn't tackle it at its simplest level and exhaust it in the four (now five, possibly six) pages that constitute a (Phys. Rev.) Letter. Already the Supplementary was turning into another paper of its own. So we decided to focus on a particular case, selecting for that purposes polaritons, which are dear objects to us, and keep the paradigm in the Letter, with the gist of our theme and a couple of illustrations. We spent the half a year or so since this publication to get to the bottom of the wider picture.
This led us to a Series of texts:
- Exciting with Quantum Light. I. Exciting an harmonic oscillator.
- Exciting with Quantum Light. II. Exciting a two-level system.
- Exciting with Quantum Light. III. Exciting polaritons.
- Exciting with Quantum Light. IV. Exciting with a bundler.
- Exciting with Quantum Light. V. Pulsed excitations.
They are still in preparation, with however the key results obtained for most of them and we are in the process of writing up. The first part has been uploaded to the arXiv this week-end and you can find it there: arXiv:1601.06187.
In the following, I will give an hopefully friendly overview of the main results of this first opus.
In this first work, we study the excitation of a quantum harmonic oscillator by a Single-photon Source (or SPS for short). The sketch above is one particular case of SPS. We studied various types of SPS but this is the most interesting one as well as possibly the simplest, so a great candidate for a fundamental study.
The first thing we did is to chart the Hilbert space of the Harmonic oscillator, i.e., provide a map to see where you are in this huge place that defies human's imagination. We find that using the population $n_a=\langle\ud{a}a\rangle$ as one ruler and the second-order correlation $g^{(2)}=\langle\ud{a}\ud{a}aa\rangle/n_a^2$ as the other gives an interesting snapshot of what the place looks like. We also considered other representations but found that moving in them was much more restricted than this joint population/statistics map. This is one of our key results:
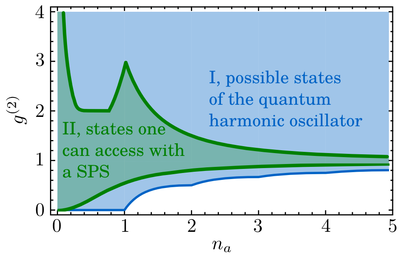
In this map of the Hilbert space, first of all, not all states are allowed. The region in white is inaccessible, and we provide the closed-form expression for the boundary:
\begin{equation}
\label{eq:miéoct21181551CEST2015}
g^{(2)}=\frac{\lfloor n_a\rfloor(2n_a-\lfloor n_a\rfloor-1)}{n_a^2}\,,
\end{equation}
along with the proof that the region above, I, is full (i.e., there always exists at least one physical state in the blue region). Now that we know where we could go, we have to see where we can go with a SPS. That is, we answer the question: what are the quantum states that you can drive a quantum oscillator into? If you have a SPS as sketched above, this is the green region II. This is a strange territory, that has this shape because it is a patch of various areas reached by the SPS in different regimes:
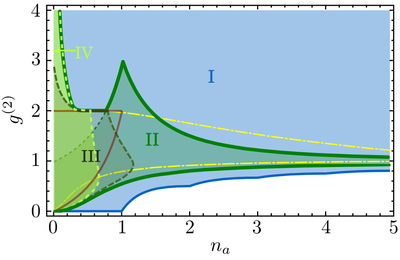
Region II is obtained with the SPS at resonance with the oscillator, IV that opens a flank of low population, high values of $g^{(2)}$ is when exciting with the leapfrog process of the source in the Mollow triplet regime (high pumping) and III is when exciting with the satellites of the latter regime, which covers a little area around $n_a\approx0.6$ and $g^{(2)}$ close to 2. For comparison and perspective, here we also put the region accessible by i) cavity QED setups where the quantum system is buried inside the oscillator and has possibly reversible exchanges with it (this is the region between the yellow dash-dotted lines) and also by ii) an incoherent SPS. The area covered by an incoherent excitation, by the way, can be identified exactly, it is bounded by below by $g^{(2)}\ge2n_a/(3-2n_a)$ and by above by $g^{(2)}\le2$. As you can see, this restrain the maximum number of excitations in the oscillator to unity, unlike the coherent case that can fit in an arbitrary number of particles (provided parameters are chosen accordingly).
Note that while the incoherent SPS is contained fully by its more versatile coherent counterpart, the cavity QED configuration gives access to states not possible by quantum excitation with a SPS. But, also vice-versa. In particular, you get closer to the whitish limit of the maximum antibunching possible for a given population, so if you like to get to the edges of things, don't think cavity QED, which requires very delicate engineering, e.g., bringing the emitter with nanometer precision at the precise location where it can overlap with the photon field of a cavity. It is actually simpler to drive your system from outside (but quantum mechanically). Easy.
These are the main results of this opening series of a work of which you will be hearing a lot, at least from me, in the coming months. I refer you to the full text for details (and more results).