Here is a short hack to turn Mathematica lists into hash tables.

Say that you want to apply a function $f$ to the values associated to the following keys:

list1 = {{key1, val1}, {key2, val2}, {key7, val3}}
list2 = {{key1, val4}, {key3, val5}}
list3 = {{key2, val6}}

to have

{{key1, f[val1, val4]}, {key2, f[val2, val6]}, {key3, f[val5]}, {key7, f[val3]}}

The following function does just this:

HashList[op_, lists_] := 
 Table[{#[[1, 1]], op @@ #[[2]]}&[
 (Transpose[Select[Join @@ lists, #[[1]] == key &]])],
      {key, Union[(Join @@ lists)[[All, 1]]]}]

You use it as

HashList[f, {list1, list2, list3}]

If you had invoked

HashList[Plus, {list1, list2, list3}]

you'd get:

{{key1, val1+val4}, {key2, val2+val6}, {key3, val5}, {key7, val3}}

2 January 2025 Depending on what type of function you want to apply, you can op@@ or op@. For instance, to compute error bars on a list such as:

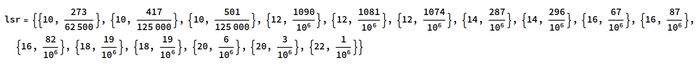
then you could first redefine the function:

HashList[op_, lists_] := 
 Table[{#[[1, 1]], op@#[[2]]} &[(Transpose[
     Select[Join @@ lists, #[[1]] == key &]])], {key, 
   Union[(Join @@ lists)[[All, 1]]]}]

Then

lmσ = HashList[Around[Mean[#], StandardDeviation[#]] &, {lsr}]

(note that we use a single list here). This is how it looks (along with a fit in red):

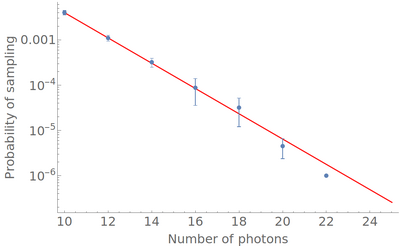
This tells me it'd take about ten million samplings, or about ten days, to get a single 24-photon realization. I could get one 22-photon realization in a day of computation (parallelized over 24 cores). Here it is: