The o-index
m |
m |
||
| Line 1: | Line 1: | ||
| − | A paper by Dorogovtsev & Mendes in Nature Physics | + | A paper by Dorogovtsev & Mendes in Nature Physics{{cite|dorogovtsev15a}} replaces the $h$-index metric (at least $h$ papers cited $h$ times) by the $o$-index, that measures a scientist's impact and productivity through their $\sqrt{hm}$ with $m$ the number of citations to their most quoted paper. |
| + | --more-- | ||
| − | It is an interesting variation in the already large family of [https://en.wikipedia.org/wiki/H-index#Alternatives_and_modifications Author-level metrics], in particular because it is so easy to compute. It is certainly one important attribute of such metrics that one should be able to compute his score immediately (my $o$-index at the time of writing is $o=\sqrt{390\times 21}=90.5$ according to Google | + | It is an interesting variation in the already large family of [https://en.wikipedia.org/wiki/H-index#Alternatives_and_modifications Author-level metrics], in particular because it is so easy to compute. It is certainly one important attribute of such metrics that one should be able to compute his score immediately (my $o$-index at the time of writing is $o=\sqrt{390\times 21}=90.5$ according to [[Google Scholar]]). Time will show if this proposal will catch up, although the $h$-metric has proved very popular and enduring. |
| − | Since it is so conveniently computed, it is also interesting to see how various databases compare. The already mentioned [https://scholar.google.com Google Scholar] has several benefits: it is free of access and it is quite dynamic (including | + | Since it is so conveniently computed, it is also interesting to see how various databases compare. The already mentioned [https://scholar.google.com Google Scholar] has several benefits: it is free of access and it is quite dynamic (including papers just put on the [http://arxiv.org/ arXiv], for instance). Disadvantages include unreliability in some cases, e.g., [[Hawking]]'s most quoted paper is actually from [[Weinberg]]: |
<center><wz tip="Hawking's most quoted paper according to scholar has not been written by Hawking!">[[File:hawking-scholar-5Nov15.jpg|600px]]</wz></center> | <center><wz tip="Hawking's most quoted paper according to scholar has not been written by Hawking!">[[File:hawking-scholar-5Nov15.jpg|600px]]</wz></center> | ||
| − | This | + | This leads to some mistrust in Scholar that tends to inflate one's citation records (possibly people like it for this reason as well). The Dorogovtsev & Mendes' paper used the Thomson Reuters Web of Science (Core Collection) database. It is not free of access and even when you get through some institutional access, you have to struggle with a painful interface. I also find it less reliable than Scholar. A selection of important scientists was emphasized. I am comparing below the Author's results with those obtained through Scholar, where one finds most of the selected researchers (still missing are [[Ernzerhof]], [[Car]], [[Hopfield]], [[Higgs]], [[Kasteleyn]], [[Fortuin]], [[Gossard]], [[Anderson]], [[Novoselov]], [[Geim]]). The others, who are not all equally famous, are readily located on the web. For the record, this is a snapshot at the time of writing: |
<center><wz tip="The lead scientist selected for the o-index study who have a profile on Scholar. Click to open in its own window (right for a new one).">[[File:ho-scientists.jpg|750px|link=http://laussy.org/images/3/37/Ho-scientists.jpg]]</wz></center> | <center><wz tip="The lead scientist selected for the o-index study who have a profile on Scholar. Click to open in its own window (right for a new one).">[[File:ho-scientists.jpg|750px|link=http://laussy.org/images/3/37/Ho-scientists.jpg]]</wz></center> | ||
| Line 14: | Line 15: | ||
<center><wz tip="The two Burke accounts on Scholar.">[[File:two-burke.png|320px]]</wz></center> | <center><wz tip="The two Burke accounts on Scholar.">[[File:two-burke.png|320px]]</wz></center> | ||
| − | {{wl-publish: | + | |
| + | The Authors state that «{{onlinequote|The merit of a researcher is determined by his or her strongest results, not by the number of publications}}» and their metrics is fine-tuned for this purpose. However, it seems false that the $h$ factor is fragile to a long list of publications (those still have to be cited!) and even more false that the strongest result is characteristic of one's merit (those are often artificial outliers). Therefore, the $h$ metrics might still be more meaningful. An obvious indicator that one can see visually from the above snapshots is also the trend of citations: if it grows with time (cumulative impact, like [[Strogatz]]), stays constant (balancing production with impact, like [[Witten]]) or, instead, decreases (the work is on its way to oblivion, like [[May]]). No metric that I know takes this into account. This probably tells more than anything else: fast growth followed by steadiness probably tells more about your field than yourself. Discontinuity indicates a breakthrough which can be scrutinized (if a big collaboration, where do you stand in it?). Etc. It seems that $o$ is not the full story either. | ||
| + | |||
| + | == References == | ||
| + | <references /> | ||
| + | {{wl-publish: 2015-11-05 11:11:10 +0000 | Fabrice }} | ||
Revision as of 20:49, 8 October 2024
A paper by Dorogovtsev & Mendes in Nature Physics[1] replaces the $h$-index metric (at least $h$ papers cited $h$ times) by the $o$-index, that measures a scientist's impact and productivity through their $\sqrt{hm}$ with $m$ the number of citations to their most quoted paper. It is an interesting variation in the already large family of Author-level metrics, in particular because it is so easy to compute. It is certainly one important attribute of such metrics that one should be able to compute his score immediately (my $o$-index at the time of writing is $o=\sqrt{390\times 21}=90.5$ according to Google Scholar). Time will show if this proposal will catch up, although the $h$-metric has proved very popular and enduring.
Since it is so conveniently computed, it is also interesting to see how various databases compare. The already mentioned Google Scholar has several benefits: it is free of access and it is quite dynamic (including papers just put on the arXiv, for instance). Disadvantages include unreliability in some cases, e.g., Hawking's most quoted paper is actually from Weinberg:
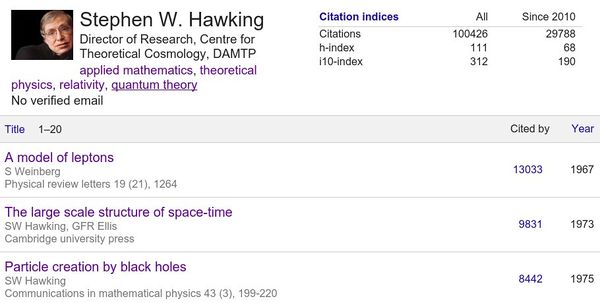
This leads to some mistrust in Scholar that tends to inflate one's citation records (possibly people like it for this reason as well). The Dorogovtsev & Mendes' paper used the Thomson Reuters Web of Science (Core Collection) database. It is not free of access and even when you get through some institutional access, you have to struggle with a painful interface. I also find it less reliable than Scholar. A selection of important scientists was emphasized. I am comparing below the Author's results with those obtained through Scholar, where one finds most of the selected researchers (still missing are Ernzerhof, Car, Hopfield, Higgs, Kasteleyn, Fortuin, Gossard, Anderson, Novoselov, Geim). The others, who are not all equally famous, are readily located on the web. For the record, this is a snapshot at the time of writing:
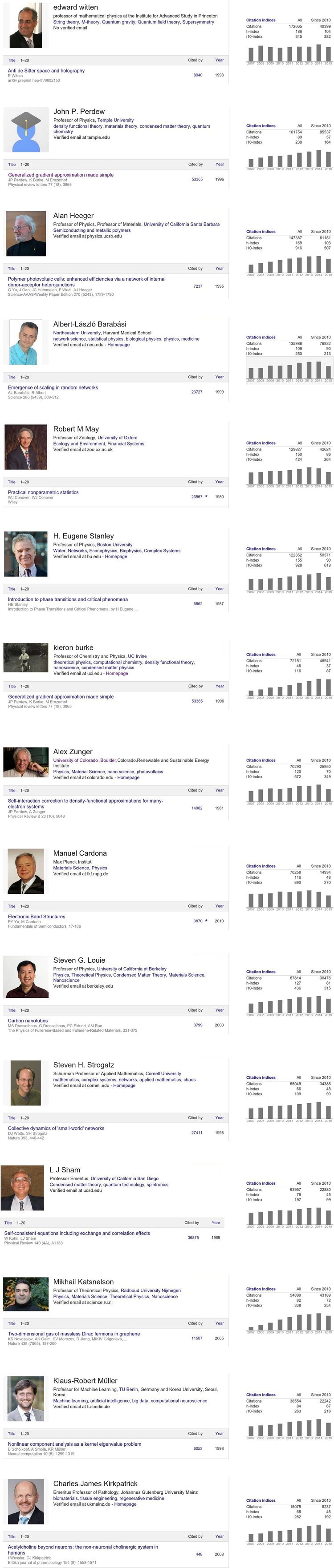
Even for these highly visible scientists, some problems are readily apparent. For instance, there are two accounts for Kieron Burke, both from the scientist in person apparently, which is a strange tolerance as it seems quite straightforward to check. They differ slightly in o-index, with baby-Burke having 1861 ($h$-index 48) and the account below 1827 ($h$ 49).

The Authors state that «The merit of a researcher is determined by his or her strongest results, not by the number of publications» and their metrics is fine-tuned for this purpose. However, it seems false that the $h$ factor is fragile to a long list of publications (those still have to be cited!) and even more false that the strongest result is characteristic of one's merit (those are often artificial outliers). Therefore, the $h$ metrics might still be more meaningful. An obvious indicator that one can see visually from the above snapshots is also the trend of citations: if it grows with time (cumulative impact, like Strogatz), stays constant (balancing production with impact, like Witten) or, instead, decreases (the work is on its way to oblivion, like May). No metric that I know takes this into account. This probably tells more than anything else: fast growth followed by steadiness probably tells more about your field than yourself. Discontinuity indicates a breakthrough which can be scrutinized (if a big collaboration, where do you stand in it?). Etc. It seems that $o$ is not the full story either.