m (→Fonts) |
m (→Shortcuts) |
||
| Line 86: | Line 86: | ||
Useful shortcuts, include: | Useful shortcuts, include: | ||
| − | * <tt>to</tt> instead of <tt>\rightarrow</tt> for $\to$ (also <tt>mapsto</tt> for $\mapsto$) | + | * <tt>\to</tt> instead of <tt>\rightarrow</tt> for $\to$ (also <tt>mapsto</tt> for $\mapsto$) |
| + | * <tt>\implies</tt> for $\implies$ | ||
== Colors == | == Colors == | ||
Revision as of 12:37, 5 January 2021

Contents |
$\mathrm{\TeX}$ and $\mathrm{\LaTeX}$
$\mathrm{\TeX}$ is one of the masterpieces of Don Knuth.
It is the uppercase version of $\tau\epsilon\chi$, a Greek word for Tech, which is how $\mathrm{\TeX}$ should be pronounced (!?).
At some point in the early 2000, I switched to $\mathrm{\LaTeX}$ for convenience, and almost exclusively use the latter now.
Equations
Alignment
Splitting equations within an aligned set can be done as followed~[1]:
\begin{align}
a &= \begin{aligned}[t]
&b + c + d +\\
&c + e + f + g + h + i
\end{aligned}\\
k &= \begin{aligned}[t]
&l + m + n\\
&+ o + p + q
\end{aligned}
\end{align}
|
\begin{align} a &= \begin{aligned}[t] &b + c + d +\\ &c + e + f + g + h + i \end{aligned}\\ k &= \begin{aligned}[t] &l + m + n\\ &+ o + p + q \end{aligned} \end{align} |
To align equations as if in a table (?!), one can use [2] This is to integrate $\int x\sin(k\pi x)dx$ by parts.
\begin{align}
u&=x & v&=-\frac{1}{k\pi}\cos(k\pi x)\\
u'&=1 & v'&=\sin(k\pi x)
\end{align}
|
\begin{align} u&=x & v&=-\frac{1}{k\pi}\cos(k\pi x)\\ u'&=1 & v'&=\sin(k\pi x) \end{align} |
To gather equations (from the Wolverhampton Lectures on Physics on Mathematics):
\begin{gather}
\mathbb{R}^n\xrightarrow[\mathbf{J}_g\atop m\times n]{g}\mathbb{R}^m\xrightarrow[\mathbf{J}_f\atop l\times m]{f}\mathbb{R}^l\\
\mathbb{R}^n\xrightarrow[\mathbf{J}_{f\circ g}\atop l\times n]{f\circ g}\mathbb{R}^l
\end{gather}
\begin{gather} \mathbb{R}^n\xrightarrow[\mathbf{J}_g\atop m\times n]{g}\mathbb{R}^m\xrightarrow[\mathbf{J}_f\atop l\times m]{f}\mathbb{R}^l\\ \mathbb{R}^n\xrightarrow[\mathbf{J}_{f\circ g}\atop l\times n]{f\circ g}\mathbb{R}^l \end{gather}
International accents
We try to write your name properly when we quote it. Here are the most common glyphs and the code needed to do so:
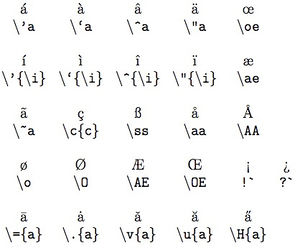
$?`$Does this work?
Fonts
See Will Robertson preambles to use different fontsets.
Shortcuts
Useful shortcuts, include:
- \to instead of \rightarrow for $\to$ (also mapsto for $\mapsto$)
- \implies for $\implies$
Colors
Using the package
\usepackage[svgnames]{xcolor}
One can then use \textcolor{red}{this is red} or \color{red} to turn everything red (until next escape).
The predefined colors are:
black, blue, brown, cyan, darkgray, gray, green, lightgray, lime, magenta, olive, orange, pink, purple, red, teal, violet, white, yellow.
but some of them are horrible! like this horrible #00ff00 pure green (so-called lime) (what it calls lime is even less visible). The svgnames gives access to about 150 additional, and pretty, colors. Use capitals letters. Here are the most useful with a short name:
|
|
|
And here are all of them.
Unicode
Unicode can be supported (at least to some extent) with
\usepackage[mathletters]{ucs}
\usepackage[utf8x]{inputenc}
It works at least for the Greek letters.
Formatting
- Wrapping figures in text: [3]
Lists
- To change spacing between items, put after \begin{itemize}:
\addtolength{\itemsep}{-0.5\baselineskip}
- To change the starting value of an enumerate list (enumii if it's a sublist):
\begin{enumerate}
\setcounter{enumi}{4}
\item fifth element
\end{enumerate}
- To change enumeration (with square brackets, parentheses, etc.): (see [4])
\usepackage{enumitem}% http://ctan.org/pkg/enumitem
\begin{document}
\begin{enumerate}[label={[\arabic*]}]
\item First item
\item Second item
\item \ldots
\item Last item
\end{enumerate}
\end{document}
Footnotes
There is a $\mathrm{\LaTeX}$ package, footmisc, that is useful for manipulating footnote formatting.
- Spacing between footnotes:
%\footnotesep is the space between footnotes:
\setlength{\footnotesep}{-0.5\baselineskip}
%\footins is the space between the text body and the footnotes:
\setlength{\skip\footins}{1cm}
- To use footnotes to feature reference-style annotations, that is, with no subscripts and with enclosing brackets [1], add in the preamble:
\makeatletter
\renewcommand{\@makefnmark}
%{\@textsuperscript{\textit{\tiny{\@thefnmark}}}}
{[\@thefnmark]}
\renewcommand\@makefntext[1]{%
\parindent 1em
\noindent
[\@thefnmark]\enspace #1}
\makeatother
(I left, commented, the original definition of the footnote).
Geometry
\usepackage[a4paper, total={6in, 8in}]{geometry}
Units
We use the siunitx package:
\usepackage{siunitx}
It'd take \SI{500}{\milli\second} to understand.
Please write \SI{10}{\micro\meter} and not 10$\mu\mathrm{m}$
There is also a SIUnits which is however deprecated [7]. Sometimes it comes in handy, for instance when you want to add non-numerical inputs (though siunitx should be able to allow that as well).
To write inverse unit, use \per:
shows the PL emission of a \SI{3}{\micro\meter} wire, where one can
observe the splitting between the two first confined subbands, the
polarization splitting, and the crossing of the X and Y (labelled TE
and TM here) polarized lines around \SI{2.6}{\per\micro\meter},
whereas the value given by the formula above is
\SI{2.1}{\per\micro\meter}.

The powers of ten can be counter-$\mathrm{\LaTeX}$-intuitive:
with a density of $\SI{e-3}{\per\square\micro\meter}$
If you do not use SI units, then omit the slash:
repetition rate of SI{3}{gb/s}
(that would be giga-bits per seconds).
Line numbering
It's useful to number profusely manuscripts of which you are discussing every line. Package lineno does that.
\usepackage{lineno}
\linenumbers

It may have a hard time cohabiting with amsmath, however. It appears that if you include this monstrosity somewhere in your preamble, it'll perform well enough for line-dropping with your co-authors:
\newcommand*\patchAmsMathEnvironmentForLineno[1]{%
\expandafter\let\csname old#1\expandafter\endcsname\csname #1\endcsname
\expandafter\let\csname oldend#1\expandafter\endcsname\csname end#1\endcsname
\renewenvironment{#1}%
{\linenomath\csname old#1\endcsname}%
{\csname oldend#1\endcsname\endlinenomath}}%
\newcommand*\patchBothAmsMathEnvironmentsForLineno[1]{%
\patchAmsMathEnvironmentForLineno{#1}%
\patchAmsMathEnvironmentForLineno{#1*}}%
\AtBeginDocument{%
\patchBothAmsMathEnvironmentsForLineno{equation}%
\patchBothAmsMathEnvironmentsForLineno{align}%
\patchBothAmsMathEnvironmentsForLineno{flalign}%
\patchBothAmsMathEnvironmentsForLineno{alignat}%
\patchBothAmsMathEnvironmentsForLineno{gather}%
\patchBothAmsMathEnvironmentsForLineno{multline}%
}
Compilation
Use texfot to get rid of the flood of output generated by compilation and retain only the warnings:
texfot pdflatex Microcavities.tex
See also
- BibTeX to manage references.
- laussy.sty my personal $\mathrm{\TeX}$ definitions.
Links
On this Web
Elsewhere on the Internet
- The Comprehensive $\LaTeX$ Symbol List of November 2015 (331 pages of glyphs).