Two-photon lasing
The analysis of the system in terms of the coherent Hamiltonian dynamics is essential in order to characterize the configurations where there is resonance with the cavity mode and the strength of the couplings giving rise to 1P and 2P oscillations. However, the efficiency and actual possibility of 2P lasing versus 1P lasing or simply against the decoherence, must be investigated taking into account pump and decay with the master equation:
As we know, one of the effects of pump and decay on the Hamiltonian
dynamics, is to average out the Rabi oscillations from the matrix
elements of the density matrix, and in particular from the populations
of all the states. The steady state can only be represented by a
mixture of all the possible final outcomes. Different manifolds of
excitation are involved in the dynamics and the mixture of states with
some probability. It is no longer possible to observe the 1P/2P
oscillations in the average populations. However, the 1PR and 2PR are
still an intrinsic feature of the system and can be studied in the
spirit of Fig. 6.19. When tuning the cavity mode over
the 1PR-2PR transitions, the intensity of the emission
![]() and
the 2P sensitive quantities
and
the 2P sensitive quantities ![]() and
and ![]() , change
dramatically as we can see in Fig. 6.20-(a) (in solid-blue,
dashed-purple and dashed-brown lines respectively). Here, we kept the
previous configuration for the QD levels (
, change
dramatically as we can see in Fig. 6.20-(a) (in solid-blue,
dashed-purple and dashed-brown lines respectively). Here, we kept the
previous configuration for the QD levels (![]() ) and some
reasonable parameters for pump and decay (
) and some
reasonable parameters for pump and decay (
![]() ,
,
![]() and
and ![]() ). The resonant energies (where the intensity
increases) are approximately the same as those given by the
Hamiltonian analysis in the case where the initial state is closer to
the biexciton (see Fig. 6.19-(b)
and 6.19-(d)). Let us discuss these results in more
detail.
). The resonant energies (where the intensity
increases) are approximately the same as those given by the
Hamiltonian analysis in the case where the initial state is closer to
the biexciton (see Fig. 6.19-(b)
and 6.19-(d)). Let us discuss these results in more
detail.
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Mean.eps}](img2031.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Pop.eps}](img2032.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Pop-detail.eps}](img2033.png) |
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Mean-gamma_0.1.eps}](img2035.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Pop-gamma_0.1.eps}](img2036.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Mean-gamma_0.3.eps}](img2037.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Pop-gamma_0.3.eps}](img2038.png) |
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Mean-gamma_0.1-chi_40.eps}](img2044.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Pop-gamma_0.1-chi_40.eps}](img2045.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Mean-chi_10.eps}](img2046.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Pop-chi_10.eps}](img2047.png) |
When the cavity mode is close to a resonance with some excitonic
transition, the system can enter a lasing regime, where
![]() and
and
![]() as we have already seen. This depends on the
strength of the couplings, either
as we have already seen. This depends on the
strength of the couplings, either ![]() for 1P lasing or the
effective coupling
for 1P lasing or the
effective coupling
![]() for 2P lasing, relatively
to the decoherence in the system. If the cavity is good enough,
for 2P lasing, relatively
to the decoherence in the system. If the cavity is good enough,
![]() (like in the case under study), the excitations
created inside can be sustained for a long time thanks to the
light-matter exchange allowing for an efficient storage of
photons. Also the QD must be far from saturation (in the biexciton in
this case) or self-quenching.
(like in the case under study), the excitations
created inside can be sustained for a long time thanks to the
light-matter exchange allowing for an efficient storage of
photons. Also the QD must be far from saturation (in the biexciton in
this case) or self-quenching.
In Fig. 6.20-(a) it is clear from the increase in
![]() and decrease in
and decrease in ![]() towards one, that both resonances bring the
system into a lasing regime. The 2PR is less efficient as the coupling
associated is weaker (
towards one, that both resonances bring the
system into a lasing regime. The 2PR is less efficient as the coupling
associated is weaker (
![]() ) than in the case of the
1PR (
) than in the case of the
1PR (![]() with two excitonic states involved). This manifests in three
ways: the maximum intensity achieved at 2PR resonance is lower, the
state is less Poissonian-like6.2 and the width of the lasing regime in terms
of the detuning
with two excitonic states involved). This manifests in three
ways: the maximum intensity achieved at 2PR resonance is lower, the
state is less Poissonian-like6.2 and the width of the lasing regime in terms
of the detuning ![]() is much narrower. When the detuning brings
the cavity mode too far from any QD level,
is much narrower. When the detuning brings
the cavity mode too far from any QD level,
![]() decays, no
lasing is produced and
decays, no
lasing is produced and ![]() becomes
becomes ![]() . We can see a clear
transition between the two lasing regimes although the two peaks
overlap and none is purely 1P or 2P lasing. Moreover,
. We can see a clear
transition between the two lasing regimes although the two peaks
overlap and none is purely 1P or 2P lasing. Moreover, ![]() decreases towards zero close to
decreases towards zero close to
![]() evidencing 1P
exchange while it is enhanced around
evidencing 1P
exchange while it is enhanced around
![]() evidencing 2P
exchange.
evidencing 2P
exchange.
In order to understand up to which extent the 2P lasing regime is
dominated by 2P dynamics, in Fig. 6.20-(b) we plot the total
populations of states ![]() (solid-blue line),
(solid-blue line), ![]() (dotted-brown) and
(dotted-brown) and ![]() (dashed-purple) as a function of
detuning. Out of any excitonic resonance, the biexciton state is
saturated by the pump. The transition into 2PR and 1P lasing is
evidenced by the deviation from this saturation (
(dashed-purple) as a function of
detuning. Out of any excitonic resonance, the biexciton state is
saturated by the pump. The transition into 2PR and 1P lasing is
evidenced by the deviation from this saturation (
![]() ). This
is why resonances excited in Fig. 6.20 are basically those of
Fig. 6.19-(b) and 6.19-(d) where the
coherent dynamics started from biexcitonic states. The other QD states
populated through the interplay with the biexciton, are the levels
involved in each lasing regime, as it was the case with the Rabi
oscillations. At
). This
is why resonances excited in Fig. 6.20 are basically those of
Fig. 6.19-(b) and 6.19-(d) where the
coherent dynamics started from biexcitonic states. The other QD states
populated through the interplay with the biexciton, are the levels
involved in each lasing regime, as it was the case with the Rabi
oscillations. At
![]() , only
, only ![]() and
and ![]() are
involved. This implies that the dynamics are driven by 1P processes
only.
are
involved. This implies that the dynamics are driven by 1P processes
only.
On the other hand, at
![]() , not only
, not only ![]() and
and
![]() participate, which would imply a 2P dynamics, but also
participate, which would imply a 2P dynamics, but also
![]() . The dynamics inside
. The dynamics inside
![]() alone does
not populate the cavity (as we could see in the derivation of the
effective Hamiltonian), but this subspace can exchange 1P with states
alone does
not populate the cavity (as we could see in the derivation of the
effective Hamiltonian), but this subspace can exchange 1P with states
![]() and
and ![]() separately even being so far from the 1PR (the
same far for both transitions
separately even being so far from the 1PR (the
same far for both transitions ![]() -
-![]() and
and
![]() -
-![]() ). At the 2PR, this 1P exchange is inefficient, as
we know, by it results in some contribution, not negligible in this
case. Therefore, the 2PR does not lead to 2P dynamics exclusively in
general, as there will always be some weak nonresonant 1P process
still present. In this case, the transition
). At the 2PR, this 1P exchange is inefficient, as
we know, by it results in some contribution, not negligible in this
case. Therefore, the 2PR does not lead to 2P dynamics exclusively in
general, as there will always be some weak nonresonant 1P process
still present. In this case, the transition ![]() and
and ![]() is
the one providing single photons as the ground state is less probably
occupied. We can conclude that the population of the ground state
is
the one providing single photons as the ground state is less probably
occupied. We can conclude that the population of the ground state
![]() is another good magnitude to identify the 2P versus 1P lasing
at the 2PR.
is another good magnitude to identify the 2P versus 1P lasing
at the 2PR.
Finally, at ![]() , some signature of the 1PR with the transition
, some signature of the 1PR with the transition
![]() and
and ![]() is expected. It appears in the logarithmic
plot of the population
is expected. It appears in the logarithmic
plot of the population ![]() , Fig. 6.20-(c), as a small
perturbation. For a case with stronger coupling (smaller
, Fig. 6.20-(c), as a small
perturbation. For a case with stronger coupling (smaller ![]() )
and less pumping (less saturation) this resonance would be more
evident.
)
and less pumping (less saturation) this resonance would be more
evident.
This discussion leads us the problem of maximizing the 2P processes so that there is a truly 2P laser operating in some clearly defined regime. There are the following points to take into account:
- The system should be in strong 2P-coupling which means a large
coupling
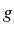 together with a good cavity so that
together with a good cavity so that
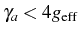 for detunings
for detunings 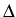 as large as
needed. However the cavity should not be so good that even at large
detuning for the 1PR, the system is still sensitive to it and
therefore the 2P lasing gets polluted with single photons. We can see
this effect in Fig. 6.21 where the cavity quality is improved
(upper figures) or worse (lower ones). In the first case, the lasing
is more efficient but both for 1P and 2P processes making it so that
the separation is not clear enough. In the second case, the separation
between the two regimes is larger but the 2P resonance does not lead
to lasing (
as large as
needed. However the cavity should not be so good that even at large
detuning for the 1PR, the system is still sensitive to it and
therefore the 2P lasing gets polluted with single photons. We can see
this effect in Fig. 6.21 where the cavity quality is improved
(upper figures) or worse (lower ones). In the first case, the lasing
is more efficient but both for 1P and 2P processes making it so that
the separation is not clear enough. In the second case, the separation
between the two regimes is larger but the 2P resonance does not lead
to lasing (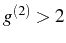 ).
).
- The pump
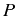 should be not so strong that the system saturates for
all detunings, quenching the production of photons at resonance. But
it should be strong enough so that in the vicinity of the 2PR, and in
particular in the transition from 2P to 1P lasing, the biexciton is
populated and the probability to be in excitonic states (that involve
0P or 1P processes) is low. This makes the transition clearer
experimentally and makes the lasing regimes purely 1P or 2P.
should be not so strong that the system saturates for
all detunings, quenching the production of photons at resonance. But
it should be strong enough so that in the vicinity of the 2PR, and in
particular in the transition from 2P to 1P lasing, the biexciton is
populated and the probability to be in excitonic states (that involve
0P or 1P processes) is low. This makes the transition clearer
experimentally and makes the lasing regimes purely 1P or 2P.
- The binding energy
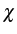 should be large enough so that the 1P
and 2P lasing regions (resonances) are far from each other and can be
resolved and considered independently. The 2P lasing efficiency is
reduced in this case, but the character of the emission seems to be
more defined (see how
should be large enough so that the 1P
and 2P lasing regions (resonances) are far from each other and can be
resolved and considered independently. The 2P lasing efficiency is
reduced in this case, but the character of the emission seems to be
more defined (see how 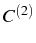 in upper Fig. 6.23-(a) is
large and distinct around
in upper Fig. 6.23-(a) is
large and distinct around
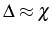 ).
). 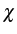 cannot be so
large, however, that the effective coupling becomes negligible at the
2PR. We can see in lower Fig. 6.21 the effect of reducing the
biexciton binding energy to
cannot be so
large, however, that the effective coupling becomes negligible at the
2PR. We can see in lower Fig. 6.21 the effect of reducing the
biexciton binding energy to 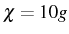 . The effective 2P coupling is
stronger and therefore at the 2PR (
. The effective 2P coupling is
stronger and therefore at the 2PR (
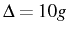 ) the lasing is more
intense with
) the lasing is more
intense with 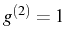 , but the two lasing regions are superimposed
making it impossible to assert that the system is dominated by 2P
processes.
, but the two lasing regions are superimposed
making it impossible to assert that the system is dominated by 2P
processes.
All these effects together could be summarized in the conditions for
the best system: A large biexcitonic extra energy ![]() balanced with
a reasonable good cavity. The optimum pumping depends on the
goal. More efficient lasing requires high pumping while a more quantum
2P emission happens at low pump.
balanced with
a reasonable good cavity. The optimum pumping depends on the
goal. More efficient lasing requires high pumping while a more quantum
2P emission happens at low pump.
Elena del Valle ©2009-2010-2011-2012.


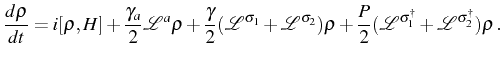
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Mean-P_1.eps}](img2040.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Mean/Pop-P_1.eps}](img2041.png)