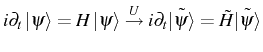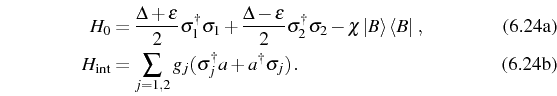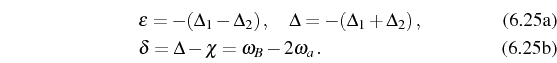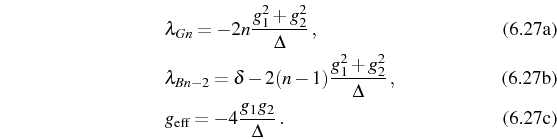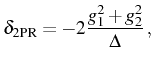Effective Hamiltonian close to the two-photon resonance
In order to derive an effective Hamiltonian, first, we make a change
of the reference frame to the cavity frequency ![]() . The unitary
operator of the transformation reads
. The unitary
operator of the transformation reads
![]() , and it is constructed such that
, and it is constructed such that
with
| (6.24) |
where
Here, we have introduced the detunings
In order to study the new 2PR condition and the strength of the
effective coupling that it induces, we take the limit
![]() , where the 2PR can be achieved and 1PR
suppressed. An effective Hamiltonian can be
obtained,
, where the 2PR can be achieved and 1PR
suppressed. An effective Hamiltonian can be
obtained,
![]() ,
within perturbation theory up to second order, which decouples the
subspaces
,
within perturbation theory up to second order, which decouples the
subspaces
![]() (with
two photon exchange between states) and
(with
two photon exchange between states) and
![]() (with no photon
exchange). The effective Hamiltonian for the two photon exchange at
fixed excitation number
(with no photon
exchange). The effective Hamiltonian for the two photon exchange at
fixed excitation number ![]() is given by
is given by
with
The two photon resonant condition
![]() , or in
terms of detunings,
, or in
terms of detunings,
is independent of the manifold, that is, of the number of photons in the cavity. When this condition is satisfied (for the cavity mode placed at
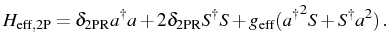 |
(6.30) |
Similarly, one can determine the effective Hamiltonian in the subspace
![\includegraphics[width=0.48\linewidth]{chap6/2P/Rabi1/Rabi-d_0-B_0.eps}](img1973.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Rabi1/Rabi-d_2.5-B_2.5.eps}](img1974.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Rabi1/Rabi-d_10-B_10.eps}](img1975.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Rabi1/Rabi-d_10-B_10-no-SS.eps}](img1976.png) |
However, for intermediate values of ![]() , in general all the QD
levels get populated and 1P oscillations between the subspaces
, in general all the QD
levels get populated and 1P oscillations between the subspaces
![]() and
and
![]() also take
place. Keeping in mind the effective physics that we have just
obtained, let us analyze the possible situations depending on the
exciton detuning
also take
place. Keeping in mind the effective physics that we have just
obtained, let us analyze the possible situations depending on the
exciton detuning ![]() and the biexciton binding energy
and the biexciton binding energy ![]() , by
plotting the Rabi oscillations of the total Hamiltonian. We consider
the dynamics inside the manifold with two excitations given by the
states
, by
plotting the Rabi oscillations of the total Hamiltonian. We consider
the dynamics inside the manifold with two excitations given by the
states
![]() . The population
of each of these states,
. The population
of each of these states, ![]() , from the initial state
, from the initial state
![]() , is given by
, is given by
![]() . We
suppose that the coupling constants and detunings of the two excitons
are equal (
. We
suppose that the coupling constants and detunings of the two excitons
are equal (![]() ,
,
![]() and
and
![]() ). In Fig. 6.16, the population of
). In Fig. 6.16, the population of ![]() is plotted in solid-blue lines, that of
is plotted in solid-blue lines, that of ![]() in dotted-brown,
and the sum of the populations of
in dotted-brown,
and the sum of the populations of
![]() and
and
![]() in
dashed-purple. The last magnitude (
in
dashed-purple. The last magnitude (
![]() ) is the total
population in the subspace
) is the total
population in the subspace
![]() and it can only
interact through 1P exchange with the other subspace. Therefore, its
oscillations are all the 1P oscillations occurring in the system. On
the other hand, oscillations in populations
and it can only
interact through 1P exchange with the other subspace. Therefore, its
oscillations are all the 1P oscillations occurring in the system. On
the other hand, oscillations in populations
![]() or
or
![]() are a mixture of 1P and 2P exchanges, only those clearly
between
are a mixture of 1P and 2P exchanges, only those clearly
between
![]() and
and
![]() are purely 2P like.
are purely 2P like.
The first case in Fig. 6.16-(a) is that of complete
resonance between all QD states and the cavity (![]() and
and
![]() ). All states 1P-oscillate and there are no 2P oscillations
due to the destructive interference. When the binding energy of the
biexciton is introduced and the 2P resonance condition achieved, 2P
oscillations appear already at small detuning,
). All states 1P-oscillate and there are no 2P oscillations
due to the destructive interference. When the binding energy of the
biexciton is introduced and the 2P resonance condition achieved, 2P
oscillations appear already at small detuning, ![]() , in
Fig. 6.16-(b). The coupling strength in the second manifold
for identical excitons is renormalized twice by a factor
, in
Fig. 6.16-(b). The coupling strength in the second manifold
for identical excitons is renormalized twice by a factor ![]() (i.e., by 2), having as a result a period for the 1P oscillations of
(i.e., by 2), having as a result a period for the 1P oscillations of
![]() . 2P oscillations are slower as the Rabi
frequency is given by
. 2P oscillations are slower as the Rabi
frequency is given by
![]() and therefore
and therefore
![]() . In this case, it is clear
also in the plot that for each 2P oscillations between
. In this case, it is clear
also in the plot that for each 2P oscillations between
![]() and
and
![]() , three 1P oscillations take place in
, three 1P oscillations take place in
![]() . The amplitude of the oscillations is inversely related
to the detuning between the cavity mode and the transition
involved. 2P oscillations occur almost with maximum amplitude while 1P
ones (off-resonance by
. The amplitude of the oscillations is inversely related
to the detuning between the cavity mode and the transition
involved. 2P oscillations occur almost with maximum amplitude while 1P
ones (off-resonance by ![]() ) never do. These features are
enhanced if the excitonic detuning is increased (keeping the 2P
resonance condition) as we can see in Fig. 6.16-(c) where
) never do. These features are
enhanced if the excitonic detuning is increased (keeping the 2P
resonance condition) as we can see in Fig. 6.16-(c) where
![]() . Note that the amplitude of the oscillations is
practically
. Note that the amplitude of the oscillations is
practically ![]() because we obtain the 2P resonance condition computing
and taking into account the Stark shift of the cavity mode due to the
presence of the nonresonant excitons. If this shift is not included in
the derivation, a naive 2P condition would be simply
because we obtain the 2P resonance condition computing
and taking into account the Stark shift of the cavity mode due to the
presence of the nonresonant excitons. If this shift is not included in
the derivation, a naive 2P condition would be simply
![]() . This would still lead to enhanced 2P oscillations but
with a reduced amplitude, as can be seen in Fig. 6.16-(d).
. This would still lead to enhanced 2P oscillations but
with a reduced amplitude, as can be seen in Fig. 6.16-(d).
We can conclude from the previous discussion that the larger ![]() ,
the stronger the 2P oscillations and the more suppressed the 1P
oscillations. At a large enough value of
,
the stronger the 2P oscillations and the more suppressed the 1P
oscillations. At a large enough value of ![]() , the result would be
the same as using the effective Hamiltonian (where
, the result would be
the same as using the effective Hamiltonian (where
![]() for this initial condition). The problem
associated with increasing
for this initial condition). The problem
associated with increasing ![]() , as discussed in more details in
the following sections, is that the effective coupling also becomes
weaker and the cavity must be extremely good to observe such a slow
dynamics.
, as discussed in more details in
the following sections, is that the effective coupling also becomes
weaker and the cavity must be extremely good to observe such a slow
dynamics.
![\includegraphics[width=.8\linewidth]{chap6/2P/Levels/levels-cavity-det-letters.eps}](img2005.png) |
Getting closer to the experimental situation, we fix the QD energy
levels
![]() and choose a reasonable value for
the biexciton energy
and choose a reasonable value for
the biexciton energy ![]() . We will not speak explicitly the
Stark shift in what follows in order to simplify the discussion
(writing approximate expressions for the resonance conditions) but it
is included for a completely efficient 2PR resonance.
. We will not speak explicitly the
Stark shift in what follows in order to simplify the discussion
(writing approximate expressions for the resonance conditions) but it
is included for a completely efficient 2PR resonance.
The transition between 1PR and 2PR can be evidenced by tuning the
cavity from
![]() to
to
![]() . The QD levels corresponding to both cases
are plotted in Fig. 6.17-(a) and (b)
respectively. The evolution of populations in the manifold with two
excitations is again shown in Fig. 6.18 in order to
appreciate the qualitative change in the dynamics when tuning the
cavity mode. In Fig. 6.18(a), we can see the oscillations
in the configuration of Fig. 6.17(a) that
correspond to 1P exchange only between states
. The QD levels corresponding to both cases
are plotted in Fig. 6.17-(a) and (b)
respectively. The evolution of populations in the manifold with two
excitations is again shown in Fig. 6.18 in order to
appreciate the qualitative change in the dynamics when tuning the
cavity mode. In Fig. 6.18(a), we can see the oscillations
in the configuration of Fig. 6.17(a) that
correspond to 1P exchange only between states ![]() and
and
![]() . The oscillations in the other extreme configuration of
Fig. 6.17(b) are plotted in
Fig. 6.16-(d). The intermediate cases where the QD
transitions are not in resonance with the energy of 1 nor 2 photons,
are those in Fig. 6.18-(b) and (c). We can see that 2P
oscillations appear clearly only when the cavity is brought very close
to the 2PR condition (
. The oscillations in the other extreme configuration of
Fig. 6.17(b) are plotted in
Fig. 6.16-(d). The intermediate cases where the QD
transitions are not in resonance with the energy of 1 nor 2 photons,
are those in Fig. 6.18-(b) and (c). We can see that 2P
oscillations appear clearly only when the cavity is brought very close
to the 2PR condition (
![]() ). This can be also seen in
a more precise way in Fig. 6.19-(a), where we plot the
amplitude of the oscillations in the populations as a function of
detuning
). This can be also seen in
a more precise way in Fig. 6.19-(a), where we plot the
amplitude of the oscillations in the populations as a function of
detuning ![]() . The broad peak sitting at
. The broad peak sitting at ![]() affects only
populations
affects only
populations ![]() and
and ![]() , while at
, while at
![]() the
peak is very narrow and affects populations
the
peak is very narrow and affects populations ![]() and
and ![]() . The
first one corresponds to a 1PR and the second to the 2PR.
. The
first one corresponds to a 1PR and the second to the 2PR.
![\includegraphics[width=0.45\linewidth]{chap6/2P/Rabi2/Rabi-d_0-B_10.eps}](img2015.png)
![\includegraphics[width=0.45\linewidth]{chap6/2P/Rabi2/Rabi-d_5-B_10.eps}](img2016.png)
![\includegraphics[width=0.45\linewidth]{chap6/2P/Rabi2/Rabi-d_9-B_10.eps}](img2017.png)
![\includegraphics[width=0.45\linewidth]{chap6/2P/Rabi2/Rabi-d_9.5-B_10.eps}](img2018.png) |
Note that if the cavity energy is further tuned down to
![]() (see Fig. 6.17-(c)), the 1P resonance is
again satisfied for the transition between states
(see Fig. 6.17-(c)), the 1P resonance is
again satisfied for the transition between states ![]() and
and
![]() . In order to see these oscillations at the Hamiltonian
level, the system must be initiated in a state other than
. In order to see these oscillations at the Hamiltonian
level, the system must be initiated in a state other than
![]() . That is, a higher excitation intensity is needed to see
this second 1PR. In Fig. 6.19-(b), the amplitude of
oscillations for the initial state
. That is, a higher excitation intensity is needed to see
this second 1PR. In Fig. 6.19-(b), the amplitude of
oscillations for the initial state ![]() , shows a third broad
peak at
, shows a third broad
peak at
![]() affecting only populations
affecting only populations ![]() and
and
![]() . This is the second 1PR. The 2PR also manifests in this
configuration in the same way as starting with
. This is the second 1PR. The 2PR also manifests in this
configuration in the same way as starting with ![]() . Finally,
if the initial state is a superposition of both cases
(
. Finally,
if the initial state is a superposition of both cases
(
![]() ), the dynamics resulting is a
superposition of the previous two cases, where we can see the three
resonances with less sharp transitions among them.
), the dynamics resulting is a
superposition of the previous two cases, where we can see the three
resonances with less sharp transitions among them.
![\includegraphics[width=0.48\linewidth]{chap6/2P/Amplitudes/Ground-detuning.eps}](img2023.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Amplitudes/Biexciton-detuning.eps}](img2024.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Amplitudes/BG-detuning.eps}](img2025.png)
![\includegraphics[width=0.48\linewidth]{chap6/2P/Amplitudes/BGMix-detuning.eps}](img2026.png) |
Elena del Valle ©2009-2010-2011-2012.