Discussion
Although the spectra in the semiconductor case that are probed at
negligible electronic pumping (![]() ) with no cavity pumping at
all (
) with no cavity pumping at
all (![]() ), are in principle described by the same expression as
that of the SE case used in the atomic model, in practise, however,
both of these conditions can be easily violated. The renormalization
of
), are in principle described by the same expression as
that of the SE case used in the atomic model, in practise, however,
both of these conditions can be easily violated. The renormalization
of ![]() with
with ![]() brings significant corrections well in the
regime where
brings significant corrections well in the
regime where ![]() ,
, ![]() and one could think that the pump is
negligible. For instance, for parameters of point (c) in
Fig. 3.9 with
and one could think that the pump is
negligible. For instance, for parameters of point (c) in
Fig. 3.9 with ![]() , the rate
, the rate ![]() that
is needed to bring a
that
is needed to bring a ![]() correction to
correction to ![]() yields,
according to Eqs. (3.15a)
and (3.15b), average populations much below
unity, namely,
yields,
according to Eqs. (3.15a)
and (3.15b), average populations much below
unity, namely,
![]() and
and
![]() . By the time
. By the time ![]() reaches unity,
with
reaches unity,
with ![]() still one fourth smaller, the correction on the effective
decay rate has became 400%. Because of thermal fluctuations in the
particle numbers, for these average values, the results are already
irreconcilable with a SE emission case. They are, as we shall see in
the next Chapter, also irreconcilable with a Fermion model. As this
is
still one fourth smaller, the correction on the effective
decay rate has became 400%. Because of thermal fluctuations in the
particle numbers, for these average values, the results are already
irreconcilable with a SE emission case. They are, as we shall see in
the next Chapter, also irreconcilable with a Fermion model. As this
is ![]() which is proportional to the signal detected in the
laboratory, the electronic pumping must be kept very small so that
corrections to the effective linewidth can be safely neglected. As
regimes with high occupation numbers are reached, the renormalized
which is proportional to the signal detected in the
laboratory, the electronic pumping must be kept very small so that
corrections to the effective linewidth can be safely neglected. As
regimes with high occupation numbers are reached, the renormalized
![]() s become very different from the bare
s become very different from the bare ![]() s in this model.
s in this model.
Second, even in the vanishing electronic pumping limit, it must be
held true that ![]() is zero. Even if only an electronic pumping is
supplied externally by the experiment, the pumping rates of the model
are the effective excitation rates of the cavity and exciton field
inside the cavity, and it is clear that photons get injected in the
cavity in structures that consists of numerous spectator dots
surrounding the one in SC
(cf. Fig. 2.2). Although most of these
dots are in WC and out of resonance with the cavity, they affect the
dynamics of the SC QD by pouring cavity photons in the system. In the
steady state, following our previous discussion, this corresponds to
changing the effective quantum state for the emission of the strongly
coupled QD. As we shall see in more detail in what follows, this bears
huge consequences on the appearance of the emitted doublet, especially
on its visibility.
is zero. Even if only an electronic pumping is
supplied externally by the experiment, the pumping rates of the model
are the effective excitation rates of the cavity and exciton field
inside the cavity, and it is clear that photons get injected in the
cavity in structures that consists of numerous spectator dots
surrounding the one in SC
(cf. Fig. 2.2). Although most of these
dots are in WC and out of resonance with the cavity, they affect the
dynamics of the SC QD by pouring cavity photons in the system. In the
steady state, following our previous discussion, this corresponds to
changing the effective quantum state for the emission of the strongly
coupled QD. As we shall see in more detail in what follows, this bears
huge consequences on the appearance of the emitted doublet, especially
on its visibility.
To fully appreciate the importance and deep consequences of these two provisions made by the SS case on its SE counterpart, we devote the rest of this Section to a vivid representation in the space of pumping and decay rates. Now that it has been made clear what is the relationship between the SE and the SS cases, we shall focus on the latter that is the adequate, general formalism to describe SC of QDs in microcavities.
In presence of a continuous, incoherent pumping, the criterion for
SC--from the requirement of energy splitting and oscillations in
the ![]() dynamics that we have discussed above--gets upgraded from
its usual expression found in the literature:
dynamics that we have discussed above--gets upgraded from
its usual expression found in the literature:
to the more general condition:
The quantitative and qualitative implications and their extent are
shown in Fig. 3.9, where we have fixed the
parameters
![]() and
and ![]() , and outlined the various
regions of interest as
, and outlined the various
regions of interest as ![]() and
and ![]() are varied (central
panel). This choice of representation allows us to investigate
configurations that can be easily imprinted experimentally in the
system: by tuning
are varied (central
panel). This choice of representation allows us to investigate
configurations that can be easily imprinted experimentally in the
system: by tuning ![]() in cavities that have different quality
factors (inversely proportional to
in cavities that have different quality
factors (inversely proportional to ![]() ).
).
The red lines enclosing the filled regions in the central plot, delimit a frontier above which the pump is so high that populations diverge (there is no steady state). This is given by the equivalent conditions that we derived in two different ways, Eqs. (3.23) and (3.36). At resonance, they simplify to
In the SC regime, the first condition is sufficient:
In the WC regime, condition (3.70b) becomes restrictive and the limiting value for
and can be interpreted as the point where the effective decay rate for mode
The main separation inside that region where a SS exists, is that
between SC (in shades of blue, inside the triangle) and WC (in shades
of red, on its right elbow). The blue solid line that marks this
boundary, is specified by
![]() , i.e., by
, i.e., by
The dashed vertical black line, specified by
corresponds to the standard criterion of SC (without incoherent pumping).
The light-blue region, labelled 1 in
Fig. 3.9, corresponds to SC as it is
generally understood. The luminescence spectrum shows a clear
splitting of the lines. The dark-blue region, labelled 2, corresponds
to SC, according to the requisite that ![]() be real, but when in the
luminescence spectrum, Eq. (3.63), only one peak is resolved.
This region is delimited by the brown line, which is the solution of
the equation
be real, but when in the
luminescence spectrum, Eq. (3.63), only one peak is resolved.
This region is delimited by the brown line, which is the solution of
the equation
![]() , i.e., no
concavity of the spectral line at the origin. From this condition
follows the implicit equation:
, i.e., no
concavity of the spectral line at the origin. From this condition
follows the implicit equation:
that yields two solutions, only one of which is physical. The other one is placed on the red line
![\includegraphics[width=0.7\linewidth]{chap3/fig10-(a,b,c)-Splitting-with-Pb.eps}](img875.png) |
In Fig. 3.11, we plot, as a function of
detuning the following magnitudes: in solid black, the bare modes
(
![]() ,
,
![]() ); in dashed black, the dressed modes
in the absence of pump and decay (
); in dashed black, the dressed modes
in the absence of pump and decay (
![]() );
in dashed blue, the system dressed modes (
);
in dashed blue, the system dressed modes (
![]() ); and in
solid red, the actual splitting of the lines in the spectra given by
the corresponding solutions of
Eq. (3.52). We do this for the cases (a),
(b), (c) and (e) of Fig. 3.9. By comparing
with the blue polariton energy lines, it is clear that both the
repulsion of the red lines in the spectra (cases c and e) and their
crossing (cases a and b) can appear both in SC (b and c) or WC (a and
e).
); and in
solid red, the actual splitting of the lines in the spectra given by
the corresponding solutions of
Eq. (3.52). We do this for the cases (a),
(b), (c) and (e) of Fig. 3.9. By comparing
with the blue polariton energy lines, it is clear that both the
repulsion of the red lines in the spectra (cases c and e) and their
crossing (cases a and b) can appear both in SC (b and c) or WC (a and
e).
The last region of SC, labelled 3, is that specified
by
![]() , i.e., that which
satisfies Eq. (3.69) but violates
Eq. (3.68), thereby being in SC according
to the more general definition that takes into account the effect of
the incoherent pumping, but that, according to the conventional
criterion, is in WC. For this reason, we refer to this region as of
pump-aided strong coupling. This is a region of strong
qualitative modification of the system, that should be in WC according
to the intrinsic system parameters (
, i.e., that which
satisfies Eq. (3.69) but violates
Eq. (3.68), thereby being in SC according
to the more general definition that takes into account the effect of
the incoherent pumping, but that, according to the conventional
criterion, is in WC. For this reason, we refer to this region as of
pump-aided strong coupling. This is a region of strong
qualitative modification of the system, that should be in WC according
to the intrinsic system parameters (
![]() ), but that
restores SC thanks to the cavity photons forced into the system.
), but that
restores SC thanks to the cavity photons forced into the system.
![\includegraphics[width=.45\linewidth]{chap3/figa--Splitting-with-det.eps}](img882.png)
![\includegraphics[width=.45\linewidth]{chap3/figb--Splitting-with-det.eps}](img883.png)
![\includegraphics[width=.45\linewidth]{chap3/figc--Splitting-with-det.eps}](img884.png)
![\includegraphics[width=.45\linewidth]{chap3/fige--Splitting-with-det.eps}](img885.png) |
We now consider the other side of the blue line, that displays the counterpart behavior in the WC. Region I is that of WC in its most natural expression. Region II, in light, is the extension into WC of featuring two maxima in the emission spectrum. In this case, this does not correspond to a line-splitting in the sense of SC where each peak is assigned to a renormalized (dressed) state, but rather to a resonance of the Fano type that is carving a hole in the single line of the weakly coupled system. In this region, one needs to be cautious not to read SC after the presence of two peaks at resonance. Finally, region III is the counterpart of region 3, in the sense that, according to the conventional criterion for the system parameters [Eq. (3.68)], this region is in SC when in reality the too-high electronic pumping has bleached it.
![\includegraphics[width=0.75\linewidth]{chap3/fig11-pyramid-2.eps}](img886.png) |
In the inset of Fig. 3.9's central panel, we reproduce the diagram to position the five points (a)-(e) in the various regions discussed, for which the luminescence spectra are displayed and decomposed into their Lorentzian (green lines) and dispersive (brown) contributions, Eqs. (3.55) and (3.57). Case (c), at the lower-left angle, corresponds to SC without any pathology nor surprise: the doublet in the luminescence spectrum--although displaced in position as shown in Fig. 3.10--is a faithful representation of the underlying Rabi-splitting. Increasing pumping brings the system into region 2 where, albeit still in SC, it does not feature a doublet anymore. The reason why, is clear on the corresponding decomposition of the spectrum, Fig. 3.9(b), with a broadening of the dressed states (in green) too large as compared to their splitting. Further increasing the pump brings it out of the SC region to reach point (a), where the two Lorentzians have collapsed on top of each other. This degeneracy of the mode emission means that the coupling only affects perturbatively each mode. As a result, the dispersive correction has vanished, and the spectrum now decomposes into two new Lorentzians centered at zero, with opposite signs [Eq. (3.64)].
Back to point (c), now keeping the pump constant and
increasing ![]() , we reach point (d). It is still in SC, although
the cavity dissipation is very large (more than four times the
coupling strength) for the small value of
, we reach point (d). It is still in SC, although
the cavity dissipation is very large (more than four times the
coupling strength) for the small value of ![]() considered. Its
spectrum of emission shows, however, a clear line-splitting that is
made neatly visible thanks to the cavity (residual)
pumping
considered. Its
spectrum of emission shows, however, a clear line-splitting that is
made neatly visible thanks to the cavity (residual)
pumping ![]() . Note that the actual separations of the two peaks is
much larger than that of the dressed states. Increasing further the
dissipation eventually brings the system into WC, but in region II
where, again due to
. Note that the actual separations of the two peaks is
much larger than that of the dressed states. Increasing further the
dissipation eventually brings the system into WC, but in region II
where, again due to ![]() , the spectrum remains a doublet. In
Fig. (e), one can see, however, that there is no Rabi splitting, and
that the two peaks arise as a result of a subtraction of the two
Lorentzians centered at
, the spectrum remains a doublet. In
Fig. (e), one can see, however, that there is no Rabi splitting, and
that the two peaks arise as a result of a subtraction of the two
Lorentzians centered at
![]() [see the WC spectrum
decomposition in Eq. (3.57)
and (3.64)]. Varying detuning for the system of point
(e), even leads to an apparent anticrossing. There is no need to
display a spectrum from region I, as in this case it does not show any
qualitative difference as compared to that of (a). Note that the
transition from SC to WC is always smooth in the observed spectra,
although it is an abrupt transition in terms of apparition or
disappearance of dressed states (due to a change of sign in a radical
in the underlying mathematical formalism).
[see the WC spectrum
decomposition in Eq. (3.57)
and (3.64)]. Varying detuning for the system of point
(e), even leads to an apparent anticrossing. There is no need to
display a spectrum from region I, as in this case it does not show any
qualitative difference as compared to that of (a). Note that the
transition from SC to WC is always smooth in the observed spectra,
although it is an abrupt transition in terms of apparition or
disappearance of dressed states (due to a change of sign in a radical
in the underlying mathematical formalism).
The schema in Fig. 3.9, constructed through Eqs. (3.71)-(3.75), contains all the physics of the system. In the following, we shall look at variations of this representation to clarify or illustrate those aspects that have been amply discussed before.
![\includegraphics[width=0.75\linewidth]{chap3/fig12-pyramid-3.eps}](img891.png) |
Fig. 3.12 shows the same diagram as that of
Fig. 3.9, only with ![]() now set to zero,
i.e., corresponding to the case of a very clean sample with no
spurious QDs other than the SC coupled one, that experiences only an
electronic pumping. Observe how, as a consequence, region 3 of SC
and II of WC have disappeared. The former was indeed the result of the
residual cavity photons helping SC. The ``pathology'' in WC of
featuring two peaks at resonance has also disappeared, but most
importantly, see how region 2 has considerably increased inside the
``triangle'' of SC, meaning that the parameters required so that the
line-splitting can still be resolved in the luminescence spectrum now
put much higher demands on the quality of the structure. This
difficulty, especially in the region where
now set to zero,
i.e., corresponding to the case of a very clean sample with no
spurious QDs other than the SC coupled one, that experiences only an
electronic pumping. Observe how, as a consequence, region 3 of SC
and II of WC have disappeared. The former was indeed the result of the
residual cavity photons helping SC. The ``pathology'' in WC of
featuring two peaks at resonance has also disappeared, but most
importantly, see how region 2 has considerably increased inside the
``triangle'' of SC, meaning that the parameters required so that the
line-splitting can still be resolved in the luminescence spectrum now
put much higher demands on the quality of the structure. This
difficulty, especially in the region where ![]() follows from the
``effective quantum state in the steady state'', that we have already
discussed. The presence of a cavity pumping, even if it is so small
that no field-intensity effects are accounted for, can favor SC by
making it visible, indeed by merely providing a photon-like character
to the quantum state. This is the manifestation in a SS of the same
influence that was observed in the SE: the luminescence spectrum of a
photon as an initial state of the coupled system, is more visible than
that of an exciton, keeping all parameters otherwise the same (see
Fig. 3.6).
follows from the
``effective quantum state in the steady state'', that we have already
discussed. The presence of a cavity pumping, even if it is so small
that no field-intensity effects are accounted for, can favor SC by
making it visible, indeed by merely providing a photon-like character
to the quantum state. This is the manifestation in a SS of the same
influence that was observed in the SE: the luminescence spectrum of a
photon as an initial state of the coupled system, is more visible than
that of an exciton, keeping all parameters otherwise the same (see
Fig. 3.6).
Another useful picture to highlight this last point, is that where the
various regions are plotted in terms of the pumping rates, ![]() and
and
![]() (see Fig. 3.13, for the line (a)-(c)
with
(see Fig. 3.13, for the line (a)-(c)
with
![]() in Fig. 3.9). The
angle of a given point with the horizontal, linked
to
in Fig. 3.9). The
angle of a given point with the horizontal, linked
to
![]() , defines the exciton-like or photon-like
character of the SS established in the system, and thus determines the
visibility of the double-peak structure of SC. This is, at low
pumpings, independent of the magnitude
, defines the exciton-like or photon-like
character of the SS established in the system, and thus determines the
visibility of the double-peak structure of SC. This is, at low
pumpings, independent of the magnitude
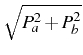 , as the
brown line defined by Eq. (3.75) is
approximately linear in this region. This shows the importance of a
careful determination of the quantum state that is established in the
SS by the interplay of the pumping and decay rates, through
Eq. (3.6). The magnitude
, as the
brown line defined by Eq. (3.75) is
approximately linear in this region. This shows the importance of a
careful determination of the quantum state that is established in the
SS by the interplay of the pumping and decay rates, through
Eq. (3.6). The magnitude
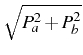 , on the other
hand, affects the splitting
, on the other
hand, affects the splitting ![]() , and the linewidth
, and the linewidth ![]() . In
order to have a noticeable renormalization, the pumps must be
comparable to the decays. On the one hand, the Rabi frequency can be
affected in different ways by the pumpings, depending on the
parameters. If
. In
order to have a noticeable renormalization, the pumps must be
comparable to the decays. On the one hand, the Rabi frequency can be
affected in different ways by the pumpings, depending on the
parameters. If
![]() , there is, in general, no effect
of decoherence on the splitting of the dressed states, showing that in
this case there is a perfect symmetric coupling of the modes into the
new eigenstates (although the broadening can be large and spoil the
resolution of the Rabi splitting anyway). If they are different, for
example in the common situation that
, there is, in general, no effect
of decoherence on the splitting of the dressed states, showing that in
this case there is a perfect symmetric coupling of the modes into the
new eigenstates (although the broadening can be large and spoil the
resolution of the Rabi splitting anyway). If they are different, for
example in the common situation that
![]() , the
Rabi increases with increasing
, the
Rabi increases with increasing ![]() . On the other hand, the
linewidth
. On the other hand, the
linewidth
![]() presents clear
bosonic characteristics: it increases with the decays but narrows with
pumping. The intensity of the pumps also affects the total intensity
of the spectra, that is proportional to
presents clear
bosonic characteristics: it increases with the decays but narrows with
pumping. The intensity of the pumps also affects the total intensity
of the spectra, that is proportional to
![]() through
through
![]() and the integration time of the apparatus. Here, however,
we have focused on the normalized spectra (i.e., the lineshape).
and the integration time of the apparatus. Here, however,
we have focused on the normalized spectra (i.e., the lineshape).
Elena del Valle ©2009-2010-2011-2012.


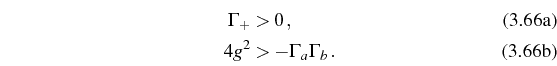
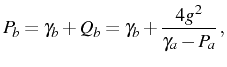 (boundary of WC),
(boundary of WC),