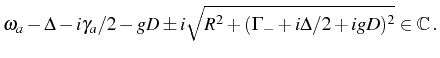Discussion
![\includegraphics[width=0.65\linewidth]{chap3/fig4-(a)-Detuning-spectraSS-d_0.eps}](img768.png)
![\includegraphics[width=0.65\linewidth]{chap3/fig4-(b)-Detuning-spectraSS-d_1.eps}](img769.png)
![\includegraphics[width=0.65\linewidth]{chap3/fig4-(c)-Detuning-spectraSS-d_3.eps}](img770.png) |
With this exposition of the analytical expressions of the luminescence
spectra, and the discussion of their similarity and distinctions that
we have just given, the coverage of the problem is complete. For
instance, Fig. 3.4 shows the SS spectra and their
mathematical decompositions into Lorentzian and dispersive parts, as
detuning is varied. Figs. (b) and (c) are obtained using
Eq. (3.37-3.40), and in this particular case, the
expression (3.50) for ![]() . The strongly coupled modes
anticross at resonance in plot (a). One feature we can observe in
these figures is how the dispersive contribution reduces as detuning
is increased. Far from resonance, the dressed modes approach the bare
ones that, being well separated in energy, also interfere
significantly less.
. The strongly coupled modes
anticross at resonance in plot (a). One feature we can observe in
these figures is how the dispersive contribution reduces as detuning
is increased. Far from resonance, the dressed modes approach the bare
ones that, being well separated in energy, also interfere
significantly less.
Given than the spectrum is a sum of contributions from the leading
modes in each regime (bare in WC or dressed in SC), the splitting in
the observed final spectrum cannot not correspond to that between the
dressed modes. Moreover, the dispersive part can contribute to an
increase of the apparent splitting or even in its appearance in weak
coupling, as I will show in the following Sections. Therefore, it is
useful from the experimental point of view to have an analytical
expression for the observed splitting that can be directly compared
with the dressed modes. For this purpose, we now solve the
equation
![]() , which provides the frequencies where the
spectrum reaches its local extrema. There exist either one or three
real solutions to this equation, corresponding to the spectrum being a
singlet or a doublet, respectively. In order to compute them, we make
use of the relation
, which provides the frequencies where the
spectrum reaches its local extrema. There exist either one or three
real solutions to this equation, corresponding to the spectrum being a
singlet or a doublet, respectively. In order to compute them, we make
use of the relation
![]() , that holds thanks
to the fact that
, that holds thanks
to the fact that
![]() . Then, the following
factorization in the complex plane is possible:
. Then, the following
factorization in the complex plane is possible:
with
Despite the simple form of Eq. (3.52), none of the roots
In order to give a more physical picture of the abstract results in
the this one and previous Sections, we shall in the rest of this
Chapter illustrate their implications in practical terms. For this
purpose, we will now concentrate on the resonant case, which is the
pillar of the SC physics. The main output of the out-of-resonance case
is to help identify or to characterize the resonance, for instance by
localizing it in an anticrossing or by providing useful additional
constrains with only one more free parameter in a global fitting. Even
a slight detuning brings features of WC into the SC system and
ultimately, when
![]() , the complex Rabi frequency converges
into the same expression for both regimes (as showed in
Fig. 3.3). This is why we now consider the SC problem in
its purest form: when the coupling between the modes is optimum.
, the complex Rabi frequency converges
into the same expression for both regimes (as showed in
Fig. 3.3). This is why we now consider the SC problem in
its purest form: when the coupling between the modes is optimum.
Elena del Valle ©2009-2010-2011-2012.


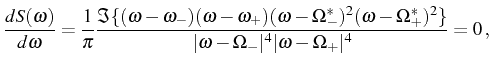
![$\displaystyle \Big[\Omega_+-\Omega_-+iW(\Omega_++\Omega_-)\pm i\sqrt{(1+W^2)(\Omega_+-\Omega_-)^2}\Big]/2$](img776.png)