Exciton-exciton scattering dynamics in a semiconductor microcavity and stimulated scattering into polaritons. F. Tassone and Y. Yamamoto in Phys. Rev. B 59:10830 (1999).  What the paper says!?

«these results must wait for further analysis beyond the rate equation, which is

beyond the scope of the present paper.»

The work details the relaxation of polaritons through Botlzmann equations. According to Hartwell & Snoke, this text «provides useful insight for those researchers doing a numerical simulation.»

This is a follow up paper to previous claims of Bose effects (their Refs. [9,10]), and its reiterated possibility:

the ob- servation of the bosonic nature of microcavity polaritons re- mained questionable. Here we instead show that it becomes

relevant in appropriate conditions.

What they mean, however, is stimulated scattering, not BEC which remains predicted as impeded by bottleneck, which is confirmed again even with more channels of relaxation:

confirmed the persistence of the bottleneck ef-

fect up to large exciton densities

Indeed, here, the Authors add to previous phonon-assisted relaxation of polaritons, the exciton-exciton (or polariton-polariton if calling them that in the flat region of their dispersion) scattering. This adds processes such as:

(1) exciton → LP 1 phonon
(2) exciton → UP6 phonon
(3) exciton 1 exciton → LP 1 exciton
(4) exciton 1 exciton → UP 1 exciton

(5) exciton 1 exciton→ LP 1 UP.

Out of which:

We identified two qualitatively different types of scattering from a dense exciton reservoir: scattering of two excitons into another ex- citon and a UP (or LP), or scattering of two excitons into

both a UP and a LP.

They discuss the relevance of the bosonic picture vs fermionic (Section II):

it is awkward (though possible) to describe an exciton condensate in the electron-

hole basis.

with references [12-14] on how to bosonize, with two-body exciton interaction as the lowest order term:

The justification is after all phe- nomenological, in that truncating up to the two-body inter- action, we achieve a satisfactory description of the dynamics

of the real system.

Their derivation of the criterion $n_\mathrm{exc}a_\mathrm{B}^2\ll1$ is very hand waving at best.

This interesting excerpt regarding the necessity of interactions should be followed up:

For thermal equilibrium, it is well known that the two-body interactions are necessary for the descrip-

tion of the second-order phase transitions.$^{16}$

Ref. [16] is S. K. Ma, Modern Theory of Critical Phenomena W. A. Benjamin, Reading, MA, 1976.

They provide references for the «actual calculation of the two-body interaction» (their Refs. [17,18,14]):

The actual calculation of the two-body interaction was already carried out in details in the literature, including the spin de-

grees of freedom.

as well as fairly detailed exposition of the microscopic scattering rates, especially in appendices.

They discretize the system in energy as opposed to momentum (compare with D. Porras et al. who argue against that and do the opposite):

we need to discretize the k space. In a finite volume calculation, the k-space mesh is uniform. However, the excitons and po- laritons have largely different masses. A dense grid for the polariton would result in an exciton grid with a prohibitively large number of points. Thus, in this paper we choose instead

a grid that is uniformly spaced in energy.

Their rate equations read (repeated indices are summed over):

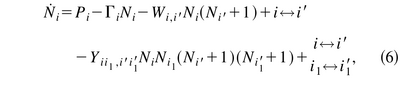
but they later simplify them into Eqs. (15-17) and even more when dealing with saturation (21-22).

It seems there is a typo in this important comment, questioning the validity of the rate equation:

intuitively, low-momentum excitations are the carrying phase over large

distances, and collision may become dependent on past ones

Solving numerically their system, they find that excitons (polaritons at high momentum) thermalize and that polaritons are strongly non-thermal, with the presence of a strong bottleneck:

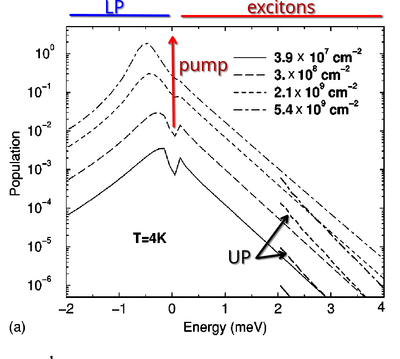
The large occupation at energies above the ground state make them speak of «a dynamical condensation» on the excited states (despite high degeneracy of those states?) They describe the dynamics as follow:

All dynamical properties of the exciton-polariton system are dominated by these two related features, the small fraction of k space occupied by polaritons,

and their small DOS.

They discuss throughout limitations of their approach, e.g.,

For exciton-exciton scattering, the scattering rate is diverging for small exchanged momenta. Thus, for these particular collisions we cannot apply the rate

equations.

including possible experimental refutations, already at the time:

recent studies put into evidence shortcomings of

the calculation of the photon emission within the simple rate-equation approach, at least for large negative detunings.$^{43}$

This is to mean what? (something deep or trivial?)

Scattering of excitons into polaritons is a unique feature of strong cou-

pling

There's a typo in Fig. 1(a) that shows their quantization of the dispersion: energy are given in units of meV (allegedely) while they appear to be eV. Also the fact they use absolute energies there but relative ones (to the exciton) later, is confusing.