Polariton dynamics and Bose-Einstein condensation in semiconductor microcavities. D. Porras, C. Ciuti, J. J. Baumberg and C. Tejedor in Phys. Rev. B 66:085304 (2002).  What the paper says!?

This is a «theoretical study of the evolution of the polariton population at large densities with a bosonic description.» The Authors derive Boltzmann equations from a microscopic Hamiltonian (in essence providing scattering rates) in a polariton-polariton picture (as opposed to phonon assisted), although the way they model the problem, that becomes exciton-polariton instead. They state that:

Exciton-polariton (X-P) scattering is identified as the most important mechanism for relaxation towards the lower polar-

iton branch.

They still also assume a phonon bath, in particular to thermalize their exciton reservoir, but this is not in their Hamiltonian, so there's a break of self-consistency there. They consider both full numerical solutions and an effective model providing analytical insights.

Their interaction Hamiltonian reads: ($a$ for photons and $b$ for excitons):

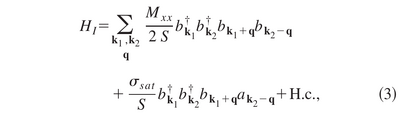
describing «Coulomb interaction between excitons and the saturation of the exciton oscillator strength», with

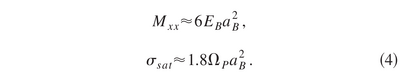
Going in the polariton basis and neglecting the upper polariton branch, they find:

From that they arrive to their Boltzmann equations:

Details are given on their quantization procedure, and they provide evidence this has modest influence on the result (their Fig. 11), which is a nice [and honest] input:

They consider of the order of a thousand polariton levels.

There's an interesting reference to a polariton trap concept, introduced earlier by Baumberg  et al..

They use CdTe systems as «the threshold for BEC can be reached for densities well below the saturation density».

There's a nice review of Bose stimulation effects of polaritons at the time, starting with:

Stimulated scattering due to the bosonic nature of polaritons has been demonstrated [4] in pump-probe experiments. Para- metric amplification and parametric oscillation, under reso- nant excitation, has been observed [5,6] and was well explained

by coherent polariton-polariton scattering. [7–9]

They contrast the fermionic (Kira & Koch) and bosonic approaches, and claims bosonic ones to be superior.

They attribute Boltzmann descriptions to Tassone and Yamamoto, which they say «describes the evolution of the polariton population by means of a semiclassical Boltzmann equation that includes polariton–acoustical-phonon and polariton- polariton scattering.» They further say that their uniform grid in energy is not suitable and they go instead for one uniform in momentum. Tassone & Yamamoto, on the other hand, precisely quantize the energy because that makes the exciton $k$-grid too large, which is also a problem for Porras et al.:

Unfortunately, the number of levels that one has to consider for the description of the polariton dy- namics is dramatically increased, and a numerical calculation that includes all the possible polariton-polariton scattering

processes is not possible.

They therefore i) consider an equilibrium distribution (Maxwell-Boltzmann rather than Bose-Einstein as $N^x\ll1$ in their case) for polaritons of the exciton type

which is a result found previously by Tassone & Yamamoto (not credited for that here), and who also later use it (but first establish it) and ii) they reduce the relaxation to this process alone, whereby «: two excitons scatter in the reservoir, and the final states are a lower polariton and another reservoir exciton»:

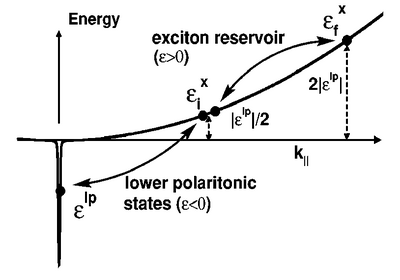
Later on, they proceed with full numerical solutions; the interplay of what is what requires a careful reading. Hartwell & Snoke apparently criticize the claim of simplification by energy quantization, as being equivalent in 2D as k-space quantization.

They neglect upper polaritons in the scattering processes, due to the very small DOS as compared to excitons, noting that:

for negative or zero detunings, the upper polariton population remains negligible, as shown experimentally [14]

and theoretically [18].

Ref. [14] is Le Si Dang (1998) while [18] is Tassone (1999), with experiment showing the way, in contrast to earlier predictions predicting stronger upper-polariton emission.

For intermediate pump powers, occupation numbers larger than 1 are obtained for modes with $k\neq0$. Thus, our model predicts

the stimulation towards these modes before BEC is achieved.

This, they say, was observed in Ref. . Their model describe the relaxation as follows:

The saturation of the emission at a given angle is related to the evolution of the polariton population that ‘‘shifts downwards’’ in energy due to the heating of the exciton reservoir. Thus, the emission at a given angle saturates when the peak in the polariton distri-

bution turns to smaller angles as pump power is increased.

Above the threshold for BEC, the macroscopic occupancy of a single microscopic mode opens the possibility for spontaneous symmetry breaking and the appearance of coherence in that mode. The interaction between the Bose-Einstein condensate and the low-energy polariton modes would lead then to the reconstruction of the polariton spectrum as predicted in the well-known Bogoliubov approach.31 These effects can modify the relaxation dynamics above threshold, so that our

results are not rigorous in this range.

The most favorable conditions for BEC are small po- lariton splittings, due to the smaller difference between the

bare exciton energy and the bottom of the LPB.

Our model allows to predict not only the possibility of BEC, but also quantitatively describes the evolution of the system to-

wards the ground state

They mainly plot quantities that are difficult to relate to the basic phenomenology, in confusing terms (as function of energy, typically, not identifying well the ground state). Their two principal graphs appear to be:

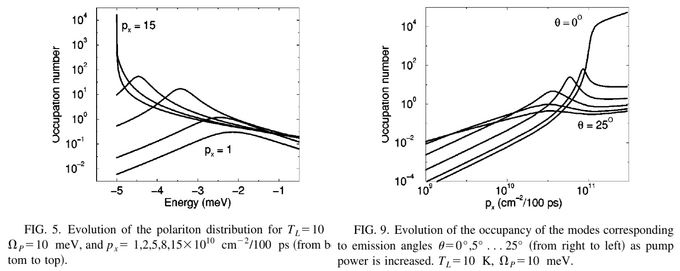
The Authors feel the need to differentiate polariton splitting from Rabi splitting (footnote 23).

Unforgivable use of the grave accent è for Règis Andrè in Ref. [3], and LaTeX typesetting that make your eyes bleed, e.g.,