Nonequilibrium condensates and lasers without inversion: Exciton-polariton lasers. A. İmamoğlu, R. J. Ram, S. Pau and Y. Yamamoto in Phys. Rev. A 53:4250 (1996).  What the paper says!?

This is one of the seminal polariton laser papers, where many of the enduring questions in the field are paused and offered with tentative answers. This comes in the wake of the experimental achievement of BEC with atoms, where also this community came up with the concept of the atom laser to distinguish the equilibrium from the non-equilibrium case. This text already defines this dichotomy as central in the problem:

Even though both of these topics [BEC & laser] have been extensively studied, little is known about their connection.

The Authors overall find that exciton lasers are possible as coherent states without inversion of population, but that a large photonic component prevents that and brings the system into a conventional photon laser, requiring population inversion. Beside those extreme, polaritonic intermediate cases where both excitons and photons play a role remains vaguely discussed.

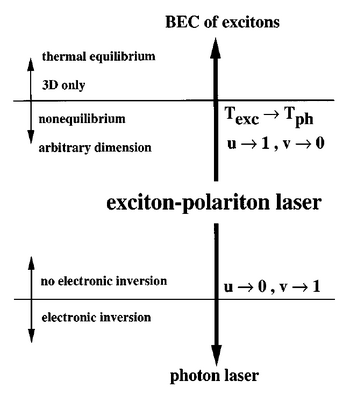
Their main three statements, in their words:

A main concern of the discussion is the relationship between BEC and lasing. The Authors claim that «for all modes that are contributing to ground-state exciton-phonon scattering, the exciton resevoir [sic] occupancy has to exceed that of the phonons.»

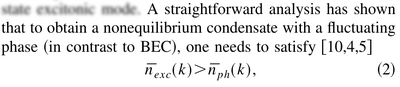
They also add a condition of population buildup:

without which, presumably, the state would not be a dim (low-population) coherent state but would remain thermal. They observe from that, that «In the equilibrium limit ($\Gamma_\mathrm{loss}\to0$), we naturally obtain the requirement for BEC.» Importantly, the Authors claim that:

In contrast to BEC, the dimensionality of the excitonic system is not important in

an exciton laser.

With hand waving arguments, they arrive at the condition:

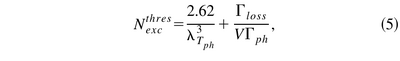
for non-equilibrium exciton condensation, which they start by saying corresponds to the «minimum reservoir exciton density N that is required to have net final state stimulated emission», but shortly after say that this «is sufficient but not necessary». So we have in short succession the two following statements:

1. «This is the first result of our letter: The observation of final-state stimulation requires an exciton density which exceeds the minimum density required for BEC».
2. «Therefore, provided that we can keep the exciton reservoir far from equilibrium, the condensation effects may be observed at densities lower than is required for BEC».

In a second part, they define an inversion operator from the exciton electron and hole number operators:

If $\langle I\rangle>0$, (wher $I$ is some averaged $I_p$ over the excitonic wavefunction), there is no electronic inversion. Assuming a coherent state, they find there can be condensation with no exciton inversion.

All this so far is for the exciton condensation, when the photonic fraction of the polariton is vanishing. They then turn to the polariton case:

For a photonlike exciton polariton, we expect two gain mechanisms to be significant: Final-state stimulation of

exciton-phonon scattering and stimulated photon emission.

Interestingly, Weisbuch's paper is not even cited here, and the references for 2D-polaritons are insted two unpublished papers by the Authors!

This is also all without interactions, that are detrimental:

The interactions between polaritons are ne- glected, since the saturation and phase diffusion caused by such interactions are not relevant to the present discus-

sion.