Bose condensation of strongly excited longitudinal electric modes. H. Fröhlich in Phys. Lett. A 26:402 (1968). What the paper says!?

In the introductory talk to the recent conference on Theoretical Physics and Biology. I have conjectured that in living systems certain coherent longitudinal electric modes are strongly excited, and stabilized by deformations arising from nonlinear effects.
This is motivated by peculiar dielectric properties of cells (of which Fröhlich elaborates little) which exhibit long-range order. The Author assumes $Z$ components coupled by dipole (long-range) interaction, each of which is supplied with energy.
His rate equation is:
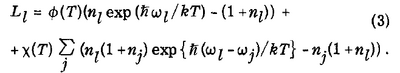
where he calls $L_l$ the loss-rate of mode $l$. This features Bose-stimulation, which is not commented upon (probably assumed obvious for longitudinal electric modes, maybe from tacit indinstinguishability arguments).
From this, in less than two pages, he proceeds to show that with increasing pumping, the total number of bosons spills out of the integral and thus a singular fraction must gather in the ground state. This is Einstein's mechanism, but out-of-equilibrium.
More discussions are given in a follow-up paper.[1]
The argument has been brought back to simple physical systems (excitons) by Tikhodeev[2] with a detour by Moskalenko.[3]
References
- ↑ Long‐range coherence and energy storage in biological systems. H. Fröhlich in Int. J. of Quant. Chem. 2:641 (1968).
- ↑ Bose condensation of finite-lifetime particles with excitons as an example. S.G. Tikhodeev in Zh. Eksp. Teor. Fiz 97:681 (1990)
- ↑ Bose condensation of phonons in biological systems. S. A. Moskalenko, E. P. Pokatilov, M. F. Miglei and E. S. Kiselyova in Int. J. of Quant. Chem. 16:745 (1979).