Area of a simple irregular polygon in polar coordinates
We discuss here the area of random simple polygons (not self-intersecting or with holes inside). The take-home message is that the area $\mathcal{A}$ of $N$ points defined in the complex plane in polar form as $z_j=re^{i\theta_j}$ with $0\le j\le N-1$ such that $0\le\theta_1\le\cdots\le\theta_N<2\pi$ is: $$\mathcal{A}={1\over2}\operatorname{Im}\sum_{i=0}^{N-1}z_iz_{(i+1)\%N}^*$$ where % means modulo, e.g., $N\%N=0$. This is something which I studied in the wake of my spatial correlations of multiphotons or the distribution of bosons in space.
The basic polygon is the triangle (for three photons). The area of a triangle whose coordinates are $(r_i,\theta_i)$ for the $i$th point ($1\le i\le 3$) such that $\theta_1\le\theta_2\le\theta_3$ with each $0\le\theta_i<2\pi$, is: [1]
$$\mathcal{A}={1\over2}\big[r_1r_2\sin(\theta_2-\theta_1)+r_2r_3\sin(\theta_3-\theta_2)-r_1r_3\sin(\theta_3-\theta_1)\big]$$
The ordering of the angles is important. The sign of the sines will subtract or add the triangles in a beautiful consistent way. Some sources make unnecessary exceptions on the possible configurations [2]. To remain on the unit circle, of course all $r_i=1$.
We can check that with Mathematica, in which case we need to define a function to properly retrieve an angle between 0 and $2\pi$ from the sine and cosine. It's a simple one but it requires ArcTan[x,y] (as opposed to ArcTan[y/x] and to take the modulo:
\[Theta]fromxy[x_, y_] := Mod[ArcTan[x, y], 2 \[Pi]]
So that defining functions GiveMeNpts to return n points on the trig circle and NAreaTrig to implement the above formula
NAreaTrig[\[Theta]1_, \[Theta]2_, \[Theta]3_] := Module[{},
1/2 (Sin[\[Theta]2 - \[Theta]1] + Sin[\[Theta]3 - \[Theta]2] -
Sin[\[Theta]3 - \[Theta]1])
]
we can check:
Similarly for polygons, someone from the triangle source suggests the formula${1\over2}\sum_{i< j} (-1)^{j-i+1}r_ir_j\sin(\theta_j - \theta_i)$ but this is wrong. The correct formula is (which is a trigonometric version of the complex-valued version above with labelling of angles between 1 and $N$):
$$\mathcal{A}={1\over2}\left[\sum_{i=1}^{N-1}r_ir_{i+1}\sin(\theta_j-\theta_i)\right]-{r_1r_N\over 2}\sin(\theta_N-\theta_1)$$ again assuming angles are in order in $[0,2\pi[$, i.e., $i<j\implies\theta_i\le\theta_j$, which is necessary for a beautiful bookkeeping of the signs of the sines.
For instance, with a 7-side polygon:
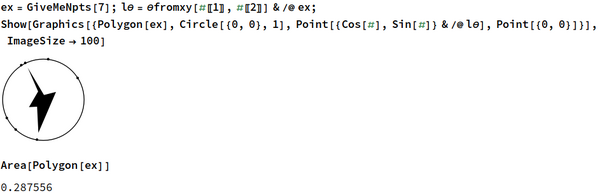
as compared to the closed-form expression:
The polygon must be simple, i.e., not self-intersecting, otherwise the formula doesn't work:
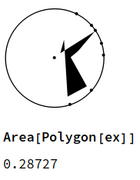
vs
You can check eligibility with the sum of angles: sum of interior angles should be $(n-2)\pi$ while sum of exteriors should be $(n+2)\pi$.