Resonance Fluorescence of a Single Artificial Atom. O. Astafiev, A. M. Zagoskin, A. A. Abdumalikov Jr., Yu. A. Pashkin, T. Yamamoto, K. Inomata, Y. Nakamura and J. S. Tsai in Science 327:840 (2010).  What the paper says!?

This is a pioneering report of resonance fluorescence—both the Heitler and Mollow regimes—of a superconducting qubit.

The two-level system is coupled to the continuum of electromagnetic modes in a 1D transmission line to avoid spatial mode mismatch between incident and scattered waves. As a result, the Authors achieve 94% power extinction (i.e., of successful coupling). In the Heitler regime, they observe that

As a single two-level system, the atom is saturated at larger powers and can have large reflectance only for the weak driving case.

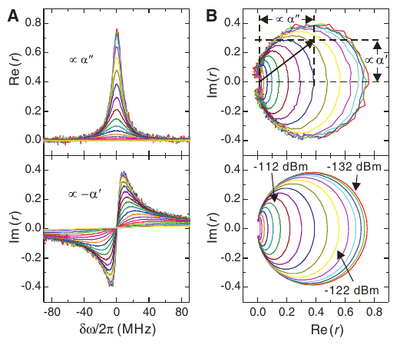
There is a nice analysis here of the reflectance (which is plotted on Schmith diagrams, whose meaning we should dig into). The scattered field (and reflected one in its wake, Eq. (2)) is simply obtained from a Lindbladian description of $\langle\sigma\rangle$. We should probably explore such results from the frequency-resolved point of view:

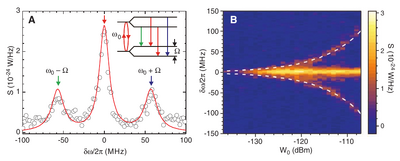
In the Mollow regime, they report a beautiful Mollow triplet in great agreement with the theory:

Some statements should be clarified:

They claim that

The situation with the atom interacting with freely propagating waves is qualitatively different from that of the atom interacting with a single-cavity mode

but do not explain in which way this differs qualitatively, and use the theory of single-mode resonance fluorescence. They also claim that

The nonlinearity of the atom manifests in the saturation of the atom excitation

which we know to be inaccurate (e.g., there is antibunching at any driving and this is a nonlinear effect, insofar as squeezing is produced and this is with no saturation). They also claim that:

The good agreement with the theory indicates the high collection efficiency of the emitted photons, which is due to the 1D confinement of the mode.

It is unclear, though, why PL, which is robust to losses, should be related in this way to collection efficiency.