Approach to Equilibrium of a Relaxing System. I. Classical 3-Level System. J. Premanand in Phys. Rev. 138:B1320 (1965).  What the paper says!?

This paper interests us for the particular case $N=3$ of our circular cascades.

She identifies the matrix of relaxation as a stochastic matrix, something which we overlooked.

She refers to a more general paper by Sudarshan.

She offers as relevant systems:

One could find an immediate applicability of the present investigation to magnetic relaxation phenomena.

She finds out (and focuses on) the circular dynamics, which is indeed the interesting case:

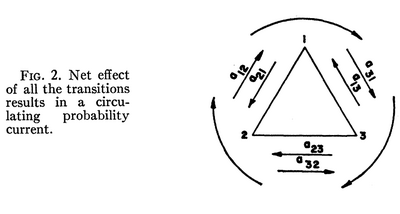
The title I. Classical 3-Level System suggests a quantum follow-up, which indeed is mentioned

The quantum analog of the system considered here will be treated in a separate paper.

but no trace of it can be found.

She thanks Sudarshan «for his comments on the paper and for many profitable suggestions and discussions.»

At the time of writing (6 February (2025)), the paper has been quoted only four times (the last time more than 50 years ago!), and it is interesting to see what the citing papers have to say about it:

1. The theory of paramagnetic relaxation. K. W. H. Stevens in Rep. Prog. Phys. 30:189 (1967).
2. An analog of the Boltzmann H-theorem (a Liapunov function) for systems of coupled chemical reactions. D. Shear in J. Theor. Biol. 16:212 (1967).
3. Modification of the Minimum-Entropy-Production Principle. P. H. E. Meijer and J. C. Edwards in Phys. Rev. A 1:1527 (1970).
4. General Properties of Thermal-Relaxation Rate Equations. M. W. P. Strandberg and J. R. Shane in Phys. Rev. B 7:4809 (1973).