Contents |
Asymmetries in Resonance Fluorescence
Kimble and Mandel[1] observed that dephasing in resonance fluorescence breaks the symmetry of the spectrum formed with a coherent, $\delta$ peak (ideal laser). This page gives a (detailed) overview of the literature on this observation.
Kimble and Mandel
This is possibly the most important paper, as the first one to report the effect.

The main finding is the great sensitivity of the spectrum itself to dephasing, as opposed to intensity correlations. The main manifestation is the reported asymmetry between the peaks. In fact, with detuning, while the spectrum itself remains symmetric, the leapfrog processes are not but they would not have known that since leapfrog would come in 2013 only.

They find analytical expressions (cf. their Eq. (50) for the spectrum, or (53) written à la Mollow) and, for the case of weak driving ($\Omega/\gamma_\sigma=0.1$), compute the following (their $\beta$ is the 2LS decay rate that we call $\gamma_\sigma$):
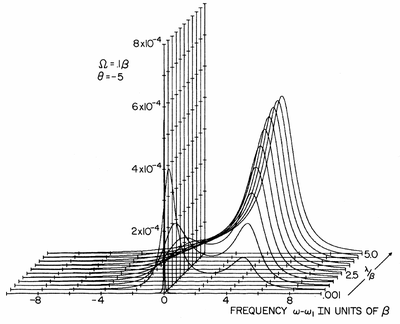
Note that we do not resolve the side-peaks and that the Rayleigh peak has a little broadening (unclear why, they might have used a trick to handle its divergence). The fluorescence is stated as "tending" towards the emitter but on the graph it appears to be pinned there. They also study the situation with the Mollow triplet, finding that there is an optimum detuning to maximize the peaks.
Knight, Molander & Stroud
Knight, Molander & Stroud[2] write a short paper to "explain" Kimble and Mandel[1]'s observation. Indeed, they make the rather strong statement (since some discussion is offered for the physical mechanism, that is even ventured as «not altogether surprising») that:
[Kimble and Mandel] offer no physical explanation for these asymmetries.
Since such asymmetries are known to occur in time-resolved situations, especially from Ref. [3], they pursue the following idea:

They use a harmonic oscillator instead of 2LS, under the rationale that this is driving so the system is almost not excited. They say that they find the same result than Kimble & Mandel, but this can only be to leading order, due to their neglecting the nonlinearity. They regard deviations as "sophistications" and comment that «The more complex theory must be used for a quantitative understanding of intermediate cases, but the physics underlying the asymmetry is still that demonstrated here.» This is overlooking the importance of such weak luminescence for two-photon observables. They make interesting comments on connections to Raman scattering (hot luminescence). They also speak of "fluctuation-induced fluorescence".
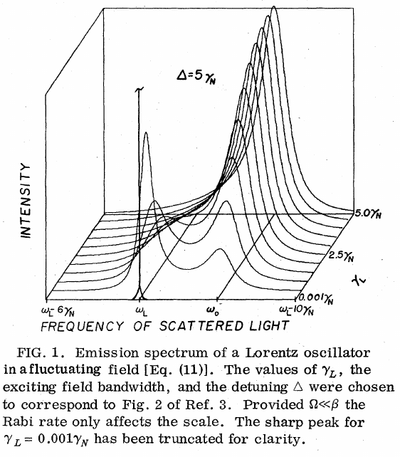
Wódkiewicz
Wódkiewicz[4] makes an independent (but later) discovery of the Kimble and Mandel effect. He doesn't quote them but is aware of related effects (for collision-induced dephasing) reported before[5][6] (his Refs. [8,10]) not cited by Kimble and Mandel. He actually cites "P.L. Knight and C.R. Stround Jr., to be published." (his Ref. [11]) which might or might not be Knight, Molander and Stroud[2]. He also makes the same approximation as them of a harmonic oscillator instead of the 2LS, with the same consequences as for them (correct spectrum to leading-order, wrong multiphoton observables). He also highlights the spectroscopic prospects of the phenomenology.
Al-Hilfy and Loudon

Al-Hilfy and Loudon[7] add, to collision broadening (homogeneous) the effect of inhomogeneous broadening, on both 1st- and 2nd-order coherence, including spectra. That describes Gaussian distributions of atomic transitions, typically due to Doppler effect. They find important qualitative differences between homogeneous and inhomogeneous broadening: homogeneous broadens the fluorescence peaks, that stay pinned at the emitter while inhomogeneous broadens in an asymmetric way the line that is also moved from the emitter towards the driving laser frequency (note: their Eq. (58) seems to have a typo, the Gaussian part should be centered on $\omega$, not $\omega_0$).
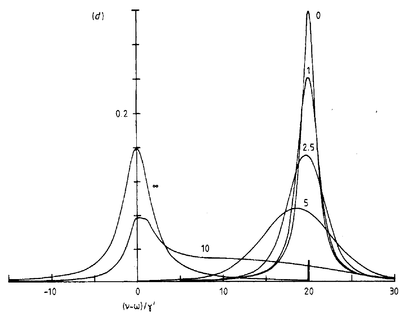
Evolution of the spectrum for $\delta/\gamma'$ with $\delta$ the width of Gaussian (inhomogeneous) broadening and $\gamma'$ the sum of radiative and pure dephasing rates. The case $0$ is the one assumed by previous authors (Lorentzian peak on the emitter) and $\infty$ turns into a Gaussian centered on the driving laser." They have a nice literature overview.
Hildred et al.

Hildred et al.[8] from the Bullough school studied driving with a coherent and thermal field. They find a transition of the spectral shape that becomes less defined (we would ourselves recover similar results in [9]):
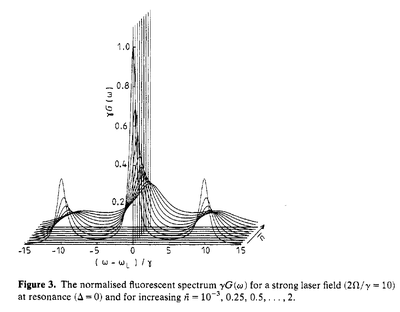
With detuning, the asymmetry is observed and becomes more marked with increasing detunings:
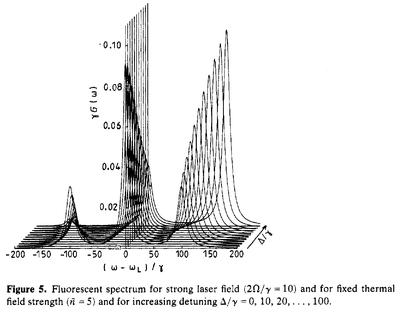
The link with the others is not entirely clear:
there appears to be a correspondence between the effect on the fluorescent spectrum of increasing the thermal field intensity $\bar n$ in our case and the effect on the spectrum of increasing the phase fluctuations of the laser driving field in Kimble and Mandel’s model.
in particular, in a footnote (on page 1712), the connection between weak and high driving is judged as not "necessarily the same":
The asymmetries in the steady-state spectra of KM have been discussed (Knight et al 1978, Raymer and Cooper 1979), but, only in the weak laser field case, in conjunction with asymmetries found in the non-stationary emission spectrum in the presence of a totally coherent field (Renaud et al 1977). Our asymmetries in the low and strong field limits are not necessarily explained along the same lines as this discussion.
Asymmetry at weak-driving: importantly, note that this is still in the high-driving regime since the central peak is still neatly visible (also from $\Omega/\gamma=0.5$):
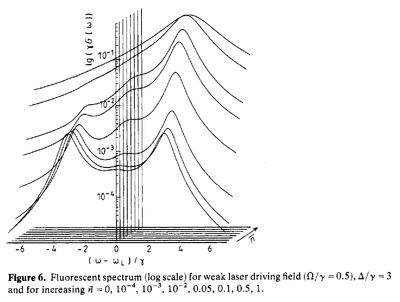
The analytical result is judged «too lengthy to write down» but seems to be provided in the appendix anyway (starting with B5).
del Valle and Laussy
The Mollow triplet is formed through the build-up of a coherent field, itself formed by the 2LS entering lasing through strong-coupling with a cavity in a Jaynes--Cummings model.[9]
References
- ↑ 1.0 1.1 Photon Antibunching in Resonance Fluorescence. H. J. Kimble, M. Dagenais and L. Mandel in Phys. Rev. Lett. 39:691 (1977).
- ↑ 2.0 2.1 Template:Knight78a
- ↑ Template:Renaud77a
- ↑ Template:Wodkiewicz78a
- ↑ Template:Huber69a
- ↑ Template:Carlsten77a
- ↑ Template:Alhilfy82a
- ↑ Thermal reservoir effects in resonance fluorescence. G. P. Hildred, S. S. Hassan, R. R. Puri and R. K. Bullough in J. Phys. B.: At. Mol. Phys. 16:1703 (1983).
- ↑ 9.0 9.1 Mollow Triplet under Incoherent Pumping. E. del Valle and F. P. Laussy in Phys. Rev. Lett. 105:233601 (2010).