m |
m |
||
| Line 428: | Line 428: | ||
As one can see, the best method worsens for $\epsilon<10^{-4}$ so it will actually work better (and faster) for not too small an $\epsilon$. | As one can see, the best method worsens for $\epsilon<10^{-4}$ so it will actually work better (and faster) for not too small an $\epsilon$. | ||
| − | < | + | <span id="newtonraphson">Let us now</span> turn to another typical numerical method: a root-finding algorithm. We used a so-called [https://en.wikipedia.org/wiki/Bisection_method bisection method] previously when generating our own random numbers, which is easy to implement but not very efficient. A simple but good improvement is the [https://en.wikipedia.org/wiki/Newton%27s_method Newton–Raphson method]. The idea is to start with a blind guess $x_0$ around the solution and replace the real function $f(x)$ by a linear approximation with the same slope at $x_0$, i.e., $h(x)=f'(x_0)x+\beta$ with $\beta$ such that $h(x_0)=f(x_0)$ which yields |
| + | |||
| + | $$h(x)=f'(x_0)[x-x_0]+f(x_0)$$ | ||
| + | |||
| + | Now a better guess for the zero is found by solving $h(x)=0$ which has solution $x=x_0-(f(x_0)/f'(x_0))$. Of course the procedure can be iterated so the algorithm gives us the always better approximations: | ||
| + | |||
| + | $$x_{n+1}=x_n-{f(x_n)\over f'(x_n)}\,.$$ | ||
| + | |||
| + | Let us find the zeros of $f(x)=\sin(x^2)$ between 0 and $\pi$. The formula gives us: | ||
| + | |||
| + | $$x_{n+1}=x_n-{\sin x^2\over 2x\cos x^2}$$ | ||
Revision as of 05:26, 26 February 2020
Crash course in Julia (programming)
Julia is a powerful/efficient/high-level computer programming language. You can get into interacting mode right-away with:
julia
Exit with exit(). One may also also use Wolfram's notebook concept:
jupyter-notebook
We will often need to install packages, which, back to julia, is done as follows:
Pkg.add("IJulia")
Then, from a terminal, jupyter-notebook opens a session in a browser, in which one can start a Julia session with a New invocation (and choosing julia there).
Let us now play with things computers are good at (e.g., with statistics). We'll need another package first:
import Pkg; Pkg.add("Distributions")
Once this is done (once for ever on a given machine), you can then be:
using Distributions
Let us generate ten thousands random points following a squared-uniform probability distribution, $X^2$.
lst=[rand()^2 for i=1:10^5]
and after
using Plots histogram(lst)
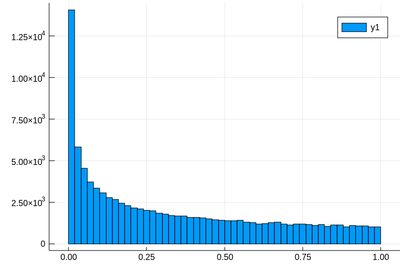
The theoretical result is obtained by differentiating the cumulative function, $f_{X^2}=dF_{X^2}/dx$, with
$$F_{X^2}(x)\equiv\mathbb{P}(X^2\le x)$$
but $\mathbb{P}(X^2\le x)=\mathbb{P}(X\le\sqrt{x})=\sqrt{x}$, since the probability is uniform. Therefore:
$$f_{X^2}(x)={1\over2\sqrt{x}}$$
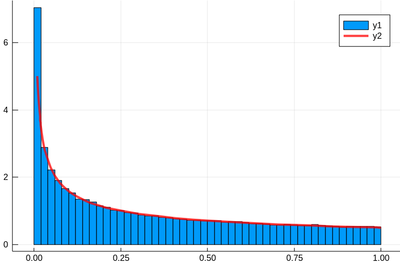
Let us check:
f(x)=1/(2*sqrt(x)) histogram(lst,norm=true) plot!(f,.01,1, linewidth = 4, linecolor = :red, linealpha=0.75)
The ! means to plot on the existing display. This seems to work indeed:
Let's have a look at the distribution of inverse random numbers, also sampled from a uniform distribution between 0 and 1. This time, the support is infinite (it is $[1,\infty[$). The theoretical distribution is $f_{1/X}=d\mathbb{P}_{1/X}/dx$ with $\mathbb{P}_{1/X}=\mathbb{P}(1/X\le x)=\mathbb{P}(X\ge 1/x)=1-1/x$ (being uniform again), so that $f_{1/X}(x)=1/x^2$.
This time we'll use a lot of points to make sure we get the exact result:
@time lst = [1/rand() for i=1:10^8]
The @time allows us to benchmark the time and memory resources involved. As you can see, on a 2020 machine, it's pretty fast (for a hundred million points!)
0.427357 seconds (67.69 k allocations: 766.257 MiB, 0.65% gc time)
The result is also consequently very smooth:
@time histogram(lst,norm=true,bins=0:.01:10)
returning
4.644046 seconds (4.88 k allocations: 1.490 GiB, 1.74% gc time)
and, after also
f(x)=1/x^2 plot!(f,1,10,linewidth=4,linecolor=:red,linealpha=.75)
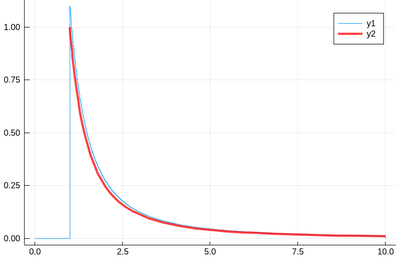
This is slightly off, clearly. The culprit is our distribution function, which density should be 1 at x=1 and is more than that. The problem is the norm option of histogram, that normalizes to what is plotted (or retained). And we have points beyond that. We can use this number to renormalize our theory plot. This is how many numbers we have:
sum(lst .< 10)
and this is the list of these numbers:
lst[lst .> 100]
Let us now explore numerically a very interesting (and important) phenomenon. For that, we'll need the Cauchy function from the above-loaded "Distributions" package. This is a histogram of $10^5$ Cauchy-distributed points:
histogram(rand(Cauchy(),10^5))
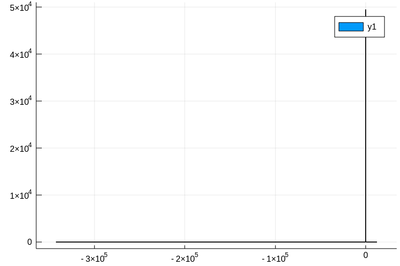
Here the binning is mandatory:
histogram(rand(Cauchy(),10^5),bins=-10:.5:10,norm=true)
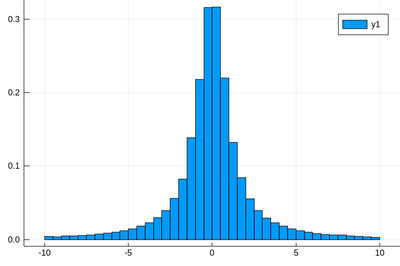
Let us now look at how to generate random numbers on our own. For instance, let us say we want to simulate the ground state of a particle in a box, with probability distribution over $[0,1]$ given by:
$$\psi^2(x)=2\sin^2(\pi x)$$
We can use unicode characters by entering \psi+TAB and call our density of probability ψ2, which in quantum mechanics is given by the modulus square of the probability amplitude (in 1D the wavefunction can always be taken real so we do not need worry about the modulus):
ψ2(x)=2*sin(pi*x)^2
That's our density of probability:
using LaTeXStrings default(; w=3) plot(ψ2,0,1, title=L"2\sin^2(x)", xlabel=L"x", ylabel=L"\psi^2(x)",dpi=150,legend=false)
where we decorated the plot with a lot of options, but the width which we gave as a default attribute, not to do it in the future (and since we like thick lines).
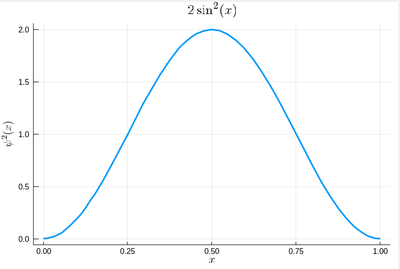
We will compute $\int_0^1\psi^2(x)\,dx$ by computing Riemann sums, i.e., as a sum of parallelograms defined in a partition of the support of the function (here $[0,1]$) cut into $n$ intervals. Calling $f$ the function to integrate, this is defined as:
$$R_n=\sum_{i=1}^{n}f(x_i)\delta(i)$$
a, b = 0, 1; # boundaries lx=range(a, stop=b, length=11) # list of x intervals δ=diff(lx) # widths of intervals lxi=lx[1:end-1] # x_i points of parallelograms
We can now check the normalization:
sum([ψ2(lxi[i])*δ[i] for i=1:length(lxi)])
1.0
The cumulative is obtained as:
Ψ=[sum([ψ2(lxi[i])*δ[i] for i=1:j]) for j=1:length(lxi)]
This is the result for 100 intervals (length=101 above):
plot(lxi, Ψ, legend=false, title="Cumulative")
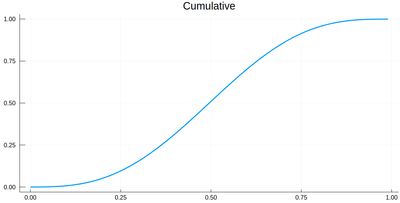
Now the generation of a random number following the initial distribution works as follows. We select randomly (uniformly) a number on the $y$-axis of the cumulative and find the corresponding $x$ such that $F(x)=y$. Those $x$ are $f$&nbps;distributed.
This can be simply achieved as follows (later we'll see a more sophisticated way):
yr=rand() fx=lx[[findmin(abs.(Ψ.-rand()))[2] for i=1:10]]
Here are some positions where our ground state collapsed:
10-element Array{Float64,1}:
0.55
0.96
0.24
0.5
0.58
0.16
0.67
0.74
0.08
0.46
histogram(lx[[findmin(abs.(Ψ.-rand()))[2] for i=1:10^7]], bins=0:.01:1,norm=true)
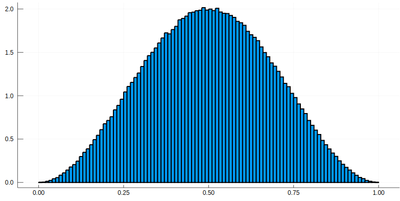
Note that the binning cannot be less than the $\delta$ step, otherwise we will get "holes" (and also the wrong normalization):
histogram(lx[[findmin(abs.(Ψ.-rand()))[2] for i=1:10^7]], bins=0:δ[1]/2:1,norm=true)
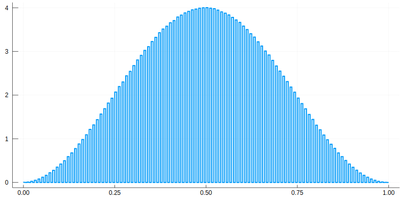
We would typically want to embed our results together in a function of our own:
function myRiemann(f, n) a, b = 0, 1; # boundaries lx=range(a, stop=b, length=n) # list of x intervals δ=diff(lx); # widths of intervals lxi=lx[1:end-1]; # x_i points of parallelograms sum([f(lxi[i])*δ[i] for i=1:length(lxi)]) end
Then we can try:
myRiemann(g, 10^3)
The result is fairly close to the exact $e-1\approx1.718281828459045$:
1.717421971020861
However we'll find that our method is fairly limited:
scatter([abs(myRiemann(g, i)-(exp(1)-1)) for i=2:100:1002], ylims=(10^-4,1), yscale=:log10, xticks=(1:11, 2:100:1002), xlabel="Num steps", ylabel="error")
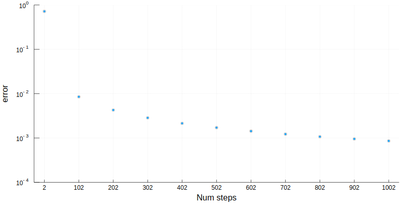
It is the purpose of numerical methods to learn how to use algorithms that are efficient, in the sense that they are accurate, fast and resource-effective.
It is easy to be brutal and terribly inefficient with a computer. In fact a fairly trivial enhancement of our method leads to considerable improvement:
function myRiemann(f, n, method="mid") a, b = 0, 1; # boundaries lx=range(a, stop=b, length=n) # list of x intervals δ=diff(lx); # widths of intervals if method == "left" lxi=lx[1:end-1]; # x_i points of parallelograms elseif method == "right" lxi=lx[2:end]; else lxi=(lx[1:end-1]+lx[2:end])/2; end sum([f(lxi[i])*δ[i] for i=1:length(lxi)]) end
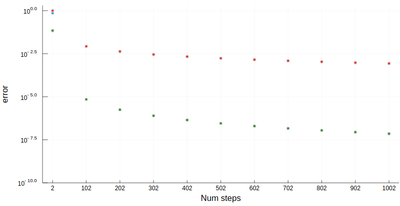
Of course, other people already wrote such functions, that are available through packages. For numerical integration of 1D functions, one can use QuadGK which is based on the so-called Gauss–Kronrod quadrature formula, which basically figures out how to best choose the points $x_i$ and how to weight them:
using QuadGK @time quadgk(g, 0, 1)
Unlike our naive implementation, the result is pretty accurate:
0.000034 seconds (9 allocations: 304 bytes) (1.718281828459045, 0.0)
That's the best we can achieve (with mid-points and a hundred-million intervals!)
@time myRiemann(g, 10^8)
9.762264 seconds (500.00 M allocations: 8.941 GiB, 11.01% gc time)
1.7182818284590453
It differs from the exact result only in the last digit, but took about 10s & 9GiB of memory.
So much for integration. How about the reverse process, i.e., derivation. We can use the diff command that computes finite differences:
diff(1:.5:10)
returns an array of 18 elements, all equal to 0.5. In this way, it is easy to compute a finite-difference derivative:
plot(diff([sin(pi*x) for x=0:.01:1])./.01)
This is a cosine. Importantly for numerical methods, one should look for simple tricks that maximise numerical accuracies. The idea behind differentiation comes from Taylor expansion:
\begin{equation} \tag{1} f(x\pm\epsilon)=f(x)\pm\epsilon f'(x)+{\epsilon^2\over2} f''(x)\pm{\epsilon^3\over6} f'''(x)+o(\epsilon^4) \end{equation}
that we wrote for both $\pm\epsilon$, and using the $o$-notation to mean that terms we neglected are of the order of $\epsilon^4$. From this, one can get an obvious numerical approximation for the derivative
$$f'(x)\approx{f(x\pm\epsilon)-f(x)\over\epsilon}+o(\epsilon)$$
meaning we can expect an error of the order of $\epsilon$ with this method. Observe however how one can sneakily cancel the $\epsilon^2$ term from (1) by subtracting $f(x-\epsilon)$ from $f(x+\epsilon)$:
$$f(x+\epsilon)-f(x-\epsilon)=2\epsilon f'(x)+{\epsilon^3\over 3}{f'''(x)}+o(\epsilon^4)$$
so that we have a much better approximation by computing with this slight variation:
$$f'(x)={f(x+\epsilon)-f(x-\epsilon)\over 2\epsilon}+o(\epsilon^2)$$
since $\epsilon^2\ll\epsilon$. The computational cost is the same, the numerical gain is considerable. Let's write a function. We'll it call Dl for "Differentiate list":
function Dl(f, δx, method="central") if method=="left" diff(f)/δx elseif method=="central" [f[i+1]-f[i-1] for i=2:length(f)-1]/(2*δx) end end
Let us compare the two methods for
δx=0.1; mysin=[sin(pi*x) for x in 0:δx:1]
We find fairly identical-looking results:
plot([Dl(mysin,δx,"central"), Dl(mysin,δx,"left")], legend=false)
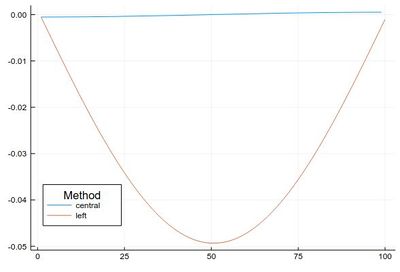
This error is actually quite large if looked at properly: (note the comparison to lists of different size, the central method removes two points)
plot([ Dl(mysin,δx,"central")-[pi*cos(pi*i) for i in δx:δx:1-δx], Dl(mysin,δx,"left")-[pi*cos(pi*i) for i in 0:δx:1-δx] ], legendtitle="Method", legend=:bottomleft, label=["central" "left"])
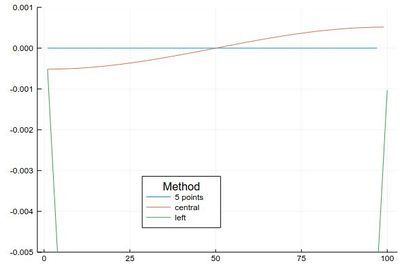
This idea (and method) can be further exploited. By working out how to cancel the next-order terms, we arrive at the so-called Five-point stencil:
$$f'(x) \approx \frac{-f(x+2\epsilon)+8 f(x+\epsilon)-8 f(x-\epsilon)+f(x-2\epsilon)}{12\epsilon}$$
which we can add to our function:
function Dl(f, δx, method="central") if method=="left" diff(f)/δx elseif method=="central" [f[i+1]-f[i-1] for i=2:length(f)-1]/(2*δx) elseif method=="fivepoints" [-f[i+2]+8f[i+1]-8f[i-1]+f[i-2] for i=3:length(f)-2]/(12*δx) end end
Comparing their errors:
plot([ Dl(mysin,δx,"fivepoints")-[pi*cos(pi*i) for i in 2δx:δx:1-2δx], Dl(mysin,δx,"central")-[pi*cos(pi*i) for i in δx:δx:1-δx], Dl(mysin,δx,"left")-[pi*cos(pi*i) for i in 0:δx:1-δx] ], legendtitle="Method", legend=:bottom, label=["5 points" "central" "left"], ylims=(-.005,.001))
If we want a more quantitative study at the errors, we can look at how it scales for various $\epsilon$. This will allow us to look at logarithmic steps:
lδx=[10.0^(-k) for k in 1:7] err1=[mean(abs.(Dl([sin(pi*x) for x in 0:δx:1], δx, "left")-[pi*cos(pi*x) for x in 0:δx:1-δx])) for δx in lδx] err2=[mean(abs.(Dl([sin(pi*x) for x in 0:δx:1], δx, "central")-[pi*cos(pi*x) for x in δx:δx:1-δx])) for δx in lδx] err3=[mean(abs.(Dl([sin(pi*x) for x in 0:δx:1], δx, "fivepoints")-[pi*cos(pi*x) for x in 2δx:δx:1-2δx])) for δx in lδx] plot([abs.(err1) abs.(err2) abs.(err3)], yscale=:log10, label=["left" "central" "5 points"], xlabel="10^-k step", ylabel="Mean abs error", lc=[:red :blue :green]) plot!([x->10.0^(-x) x->10.0^(-2x) x->10.0^(-4x)],1,7, yscale=:log10, ylims=(10^(-15),1), lc=[:red :blue :green], ls=:dash, label=["" "" ""])
with the beautiful result:
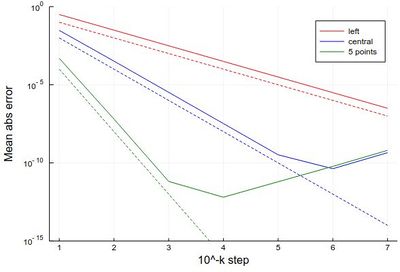
As one can see, the best method worsens for $\epsilon<10^{-4}$ so it will actually work better (and faster) for not too small an $\epsilon$.
Let us now turn to another typical numerical method: a root-finding algorithm. We used a so-called bisection method previously when generating our own random numbers, which is easy to implement but not very efficient. A simple but good improvement is the Newton–Raphson method. The idea is to start with a blind guess $x_0$ around the solution and replace the real function $f(x)$ by a linear approximation with the same slope at $x_0$, i.e., $h(x)=f'(x_0)x+\beta$ with $\beta$ such that $h(x_0)=f(x_0)$ which yields
$$h(x)=f'(x_0)[x-x_0]+f(x_0)$$
Now a better guess for the zero is found by solving $h(x)=0$ which has solution $x=x_0-(f(x_0)/f'(x_0))$. Of course the procedure can be iterated so the algorithm gives us the always better approximations:
$$x_{n+1}=x_n-{f(x_n)\over f'(x_n)}\,.$$
Let us find the zeros of $f(x)=\sin(x^2)$ between 0 and $\pi$. The formula gives us:
$$x_{n+1}=x_n-{\sin x^2\over 2x\cos x^2}$$