(Surprisingly disregarded but important paper which clarifies a lot of things) |
m |
||
| Line 23: | Line 23: | ||
<center><wz tip="Coincidence rates from the cascade for both the Franson and HOM configurations. Labels on the square brackets identify particular processes in the decomposition.">[[File:Screenshot_20240626_200709.png|500px]]</wz></center> | <center><wz tip="Coincidence rates from the cascade for both the Franson and HOM configurations. Labels on the square brackets identify particular processes in the decomposition.">[[File:Screenshot_20240626_200709.png|500px]]</wz></center> | ||
| + | |||
| + | They treat in particular two configurations, with radiative imbalances (while we tend to focus on cases where they are the same): | ||
| + | <center><wz tip="The two cases analyzed in details, disregarding the case where they are equal.">[[File:Screenshot_20240626_205028.png|400px]]</wz></center> | ||
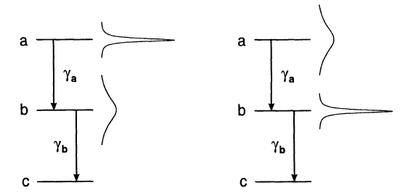
In various limits, keeping or not various terms of the interferences, this reproduce Franson, HOM and still other cases, so this represents a quite important and enlightening result. | In various limits, keeping or not various terms of the interferences, this reproduce Franson, HOM and still other cases, so this represents a quite important and enlightening result. | ||
Latest revision as of 18:59, 26 June 2024
Paradigm for Two-Photon Cascade Intensity Correlation Experiments. G. M. Meyer, G. S. Agarwal, H. Huang and M. O. Scully in Electron Theory and Quantum Electrodynamics. NATO ASI Series 358:111 (1997). What the paper says?

«Quantum electrodynamics is a spectacularly successful theory, nowhere are its successes more numerous than in modern quantum optics.»
The paper studies intensity correlation (interferometry) from the two-photon cascade emission of a single three-level atom. It identifies two basic experimental implementations:
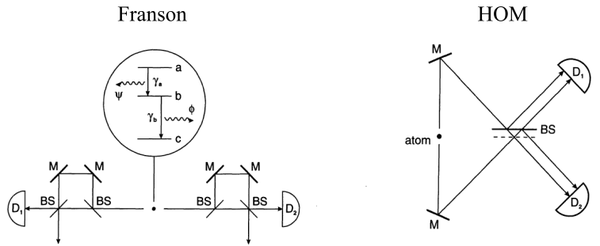
They consider a given type of quantum state for the two-photon packet and track down interferences through the two schemes, which they claim to unify:

They assume this (entangled) wavefunction:

which gives rise to the following terms in the calculation of the coincidences, in the respective two configurations:
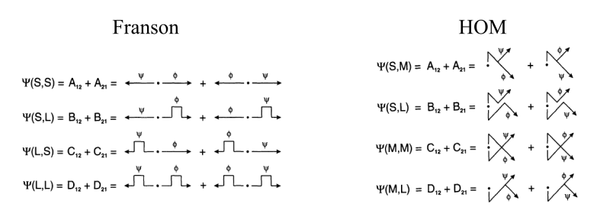
from which they arrive to (time-integrated) correlations covering both cases:

They treat in particular two configurations, with radiative imbalances (while we tend to focus on cases where they are the same):
In various limits, keeping or not various terms of the interferences, this reproduce Franson, HOM and still other cases, so this represents a quite important and enlightening result.
They also consider what they call an "interrupted cascade":
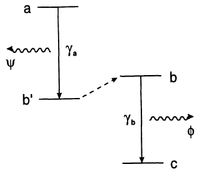
This concept is important to us as it is the opposite of our leapfrog transition. This begs the question, how does this compare the cascade above? To us, this is interrupted (by the intermediate, real state). Unfortunately, the Authors comment little about the relationships and differences, only commenting that in one limit, they have "the same dominant terms":