Julia programming
m |
m |
||
| Line 118: | Line 118: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Euler's method is not very accurate. It can be improved by considering a better estimation for the tangent. | + | Euler's method is not very accurate. It can be improved by considering a better estimation for the tangent. The idea is to use not the tangent of $y$ at $t_n$ only but also at $t_{n+1}$ and take the average: |
| − | $$y_{n+1} = y_n + {h\ | + | $$y_{n+1}=y_n+{h\over 2}[f(t_n,y_n)+f(t_{n+1},y_{n+1}]$$ |
| − | + | Of course, we do not know $y_{n+1}$, so the method would appear to become implicit, and we will deal with such a case later. But here, simply, we merely use Euler's method to estimate it: | |
| − | + | $$y_{n+1}=y_n+hf(t_n,y_n)$$ | |
| − | + | so that we have an explicit formula again: | |
| − | Heun's | + | $$y_{n+1} = y_n + {h\over2} (f(t_n, y_n) + f(t_n + h, y_n + h f(t_n, y_n)))$$ |
| + | |||
| + | This is known as Heun's method. It is one of the simplest of a class of methods called predictor-corrector algorithms (Euler's method is only a predictor method). | ||
We now cover one of the most powerful predictor-corrector algorithms of all, | We now cover one of the most powerful predictor-corrector algorithms of all, | ||
one which is so accurate that most computer algorithms use it as default: the fourth-order Runge-Kutta Method. RK methods are optimized predictor-corrector methods, so they push the idea of Heun's method to the top. | one which is so accurate that most computer algorithms use it as default: the fourth-order Runge-Kutta Method. RK methods are optimized predictor-corrector methods, so they push the idea of Heun's method to the top. | ||
| + | Let's try it on Example 3 of [http://tutorial.math.lamar.edu/Classes/DE/Bernoulli.aspx Paul's online notes]: | ||
| + | |||
| + | $$6y' - 2y = x\,{y^4}\hspace{0.25in}y\left( 0 \right) = - 2$$ | ||
| + | |||
| + | with solution: | ||
| + | |||
| + | $$y\left( x \right) = - \frac{2}{{{{\left( {4x - 4 + 5{{\bf{e}}^{ - \,x}}} \right)}^{\frac{1}{3}}}}}$$ | ||
Optimizing this method, we arrive to (in a way which we do not detail here) the so-called ''Runge-Kutta''. It involves the computation of these intermediate points: | Optimizing this method, we arrive to (in a way which we do not detail here) the so-called ''Runge-Kutta''. It involves the computation of these intermediate points: | ||
| Line 140: | Line 149: | ||
k_2 &= h\ f\left(t_n + \frac{h}{2}, y_n + \frac{k_1}{2}\right)\,, \\ | k_2 &= h\ f\left(t_n + \frac{h}{2}, y_n + \frac{k_1}{2}\right)\,, \\ | ||
k_3 &= h\ f\left(t_n + \frac{h}{2}, y_n + \frac{k_2}{2}\right)\,, \\ | k_3 &= h\ f\left(t_n + \frac{h}{2}, y_n + \frac{k_2}{2}\right)\,, \\ | ||
| − | k_4 &= h\ f\left(t_n + h, y_n + k_3\right)\, | + | k_4 &= h\ f\left(t_n + h, y_n + k_3\right)\,, |
\end{align} | \end{align} | ||
| Line 147: | Line 156: | ||
\begin{align} | \begin{align} | ||
t_{n+1} &= t_n + h\,, \\ | t_{n+1} &= t_n + h\,, \\ | ||
| − | y_{n+1} &= y_n + \tfrac{1}{6}\left(k_1 + 2k_2 + 2k_3 + k_4 \right) | + | y_{n+1} &= y_n + \tfrac{1}{6}\left(k_1 + 2k_2 + 2k_3 + k_4 \right)\,. |
\end{align} | \end{align} | ||
| + | |||
| + | In code: | ||
| + | <syntaxhighlight lang="python"> | ||
| + | @time for n=1:npts-1 | ||
| + | tn=(n-1)*h-t0; | ||
| + | k1=h*f(tn,y[n]); | ||
| + | k2=h*f(tn+(h/2),y[n]+k1/2); | ||
| + | k3=h*f(tn+(h/2),y[n]+k2/2); | ||
| + | k4=h*f(tn+h,y[n]+k3); | ||
| + | y[n+1]=y[n]+(1/6)*(k1+2*k2+2*k3+k4) | ||
| + | end | ||
| + | </syntaxhighlight> | ||
http://tutorial.math.lamar.edu/Classes/DE/Bernoulli.aspx | http://tutorial.math.lamar.edu/Classes/DE/Bernoulli.aspx | ||
Revision as of 08:39, 11 March 2020
One can generate an array from a range 1:10 using collect():
collect(1:10)
10-element Array{Int64,1}:
1
2
3
4
5
6
7
8
9
10
Let us now turn to a typical numerical problem, solving differential equations. We'll start with Ordinary Differential Equations (ODE). Namely, we consider equations of the type:
$$\tag{1} y'(t)=f(t,y(t))$$
The most famous algorithm is Euler's method and the most popular the RK4 variant of the Runge–Kutta methods. In between are a variety of possible implementations, many related in some way or the other. Methods can be explicit (the solution only depends on quantities already known) or implicit (the solution involves other unknowns which requires solving intermediate equations). The backward Euler method is an implicit method. Euler's method is the simplest one and the typical starting point to introduce the basic idea. Not surprisingly, it is also one of the least efficient. We discretize time into steps $t_1$, $t_2$, $\cdots$, $t_n$ separated by the same interval $h$. The solutions at these times are denoted $y_n=y(t_n)$. Back to (1), approximating $y'(t)\approx (y(t+h)-y(t))/h$, we have:
$$y_{n+1}=y_n+hf(t_n,y_n)$$
This is very simple since from the solution $y_n$ at time $t_n$ we can compute the solution at $t_{n+1}$. Explicitly.
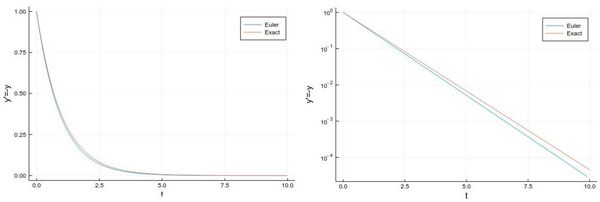
Let us solve, for instance, $y'=-y$, whose solution is the exponential function.
npts = 100; # number of points y=0.0*collect(1:npts); # predefine the array h=.1; # timesteps, so total time = npts*h=10 # The differential equation to solve function f(t,y) -y end y[1]=1; # initial condition # The numerical method (Euler's) for i=1:npts-1 y[i+1]=y[i]+h*f((i-1)*h,y[i]) end
And we can now compare the numerical solution to the real one:
plot(((1:npts).-1)*h, [y[i] for i=1:npts], label="Euler", xlabel="t", ylabel="y'=-y") plot!(x->exp(-x),0, 10, label="Exact")
Let us try the more difficult example:
$$y'={y\over 2}+2\sin(3t)\tag{2}$$
whose solution can be found with an integrating factor [1]
$$y=-{24\over37}\cos(3t)-{4\over37}\sin(3t)+\left(y(0)+{24\over 37}\right)e^{t/2}$$
In this case the differential equation is defined as:
function f(t,y) (y/2)+2sin(3t) end
The Volterra-Lotka model reads:
Euler's method in this case reads:
$$\begin{align} y_{1,n+1}&=y_{1,n}+hf_1(t_n,y_{1,n},y_{2,n})\\ y_{2,n+1}&=y_{2,n}+hf_2(t_n,y_{1,n},y_{2,n}) \end{align}$$
The functions are implemented as:
function f1(t,y1, y2) α*y1-β*y1*y2 end function f2(t,y1, y2) δ*y1*y2-γ*y2 end
npts=10000 h=.001 y1=0.0*collect(1:npts); y2=0.0*collect(1:npts); y1[1]=1; y2[1]=.1; α=2/3; β=4/3; γ=1; δ=1; @time for i=1:npts-1 y1[i+1]=y1[i]+h*f1((i-1)*h,y1[i],y2[i]) y2[i+1]=y2[i]+h*f2((i-1)*h,y1[i],y2[i]) end
plot([[y1[i] for i=1:npts], [y2[i] for i=1:npts]])
plot([(y1[i], y2[i]) for i=1:npts])
Euler's method is not very accurate. It can be improved by considering a better estimation for the tangent. The idea is to use not the tangent of $y$ at $t_n$ only but also at $t_{n+1}$ and take the average:
$$y_{n+1}=y_n+{h\over 2}[f(t_n,y_n)+f(t_{n+1},y_{n+1}]$$
Of course, we do not know $y_{n+1}$, so the method would appear to become implicit, and we will deal with such a case later. But here, simply, we merely use Euler's method to estimate it:
$$y_{n+1}=y_n+hf(t_n,y_n)$$
so that we have an explicit formula again:
$$y_{n+1} = y_n + {h\over2} (f(t_n, y_n) + f(t_n + h, y_n + h f(t_n, y_n)))$$
This is known as Heun's method. It is one of the simplest of a class of methods called predictor-corrector algorithms (Euler's method is only a predictor method).
We now cover one of the most powerful predictor-corrector algorithms of all, one which is so accurate that most computer algorithms use it as default: the fourth-order Runge-Kutta Method. RK methods are optimized predictor-corrector methods, so they push the idea of Heun's method to the top.
Let's try it on Example 3 of Paul's online notes:
$$6y' - 2y = x\,{y^4}\hspace{0.25in}y\left( 0 \right) = - 2$$
with solution:
$$y\left( x \right) = - \frac{2}{{{{\left( {4x - 4 + 5{{\bf{e}}^{ - \,x}}} \right)}^{\frac{1}{3}}}}}$$
Optimizing this method, we arrive to (in a way which we do not detail here) the so-called Runge-Kutta. It involves the computation of these intermediate points:
\begin{align} k_1 &= h\ f(t_n, y_n)\,, \\ k_2 &= h\ f\left(t_n + \frac{h}{2}, y_n + \frac{k_1}{2}\right)\,, \\ k_3 &= h\ f\left(t_n + \frac{h}{2}, y_n + \frac{k_2}{2}\right)\,, \\ k_4 &= h\ f\left(t_n + h, y_n + k_3\right)\,, \end{align}
and then the calculation is explicit:
\begin{align} t_{n+1} &= t_n + h\,, \\ y_{n+1} &= y_n + \tfrac{1}{6}\left(k_1 + 2k_2 + 2k_3 + k_4 \right)\,. \end{align}
In code:
@time for n=1:npts-1 tn=(n-1)*h-t0; k1=h*f(tn,y[n]); k2=h*f(tn+(h/2),y[n]+k1/2); k3=h*f(tn+(h/2),y[n]+k2/2); k4=h*f(tn+h,y[n]+k3); y[n+1]=y[n]+(1/6)*(k1+2*k2+2*k3+k4) end
http://tutorial.math.lamar.edu/Classes/DE/Bernoulli.aspx
http://calculuslab.deltacollege.edu/ODE/7-C-3/7-C-3-h.html
Backward Euler method, or Implicit Euler method,