Entanglement
Two degrees of freedom are entangled when the system density matrix cannot be expressed as a mixture of separable states. Besides their fundamental interest, entangled states are highly sought for applications in quantum information processing. Many such implementations might involve QDs as building blocks, as that of Awschalom et al. (2002) or Imamoglu (1999). In the following we consider the possibilities open to the system under consideration.
From the couplings that Eq. (6.9) establishes
between the different levels in the local basis, it follows that the
reduced density matrix for the QDs in the steady state takes the form:
Therefore, the only way to entangle the two dots is to populate the
Dicke states
![]() (which are two of the
so-called Bell states). In a bipartite four-level system, the degree
of entanglement can be quantified by the tangle (
(which are two of the
so-called Bell states). In a bipartite four-level system, the degree
of entanglement can be quantified by the tangle (![]() ), which
ranges from 0 (separable states) to 1 (maximally entangled states)
[see the work by Wootters (1998)]. In order to compute
), which
ranges from 0 (separable states) to 1 (maximally entangled states)
[see the work by Wootters (1998)]. In order to compute
![]() , we need to introduce the intermediate quantities
, we need to introduce the intermediate quantities ![]() and
and ![]() , defined as:
, defined as:
The tangle is then
where
We are interested in conditions that maximize ![]() : these correspond
to large values of the off-diagonal elements
: these correspond
to large values of the off-diagonal elements
![]() and small
populations of the states
and small
populations of the states
![]() . Here, dissipation and
pumping cause
. Here, dissipation and
pumping cause
![]() to evolve into a mixture, with
reduced coherences and nonzero occupancy of all levels. This limits
the maximum tangle that can be achieved as was described by
Munro et al. (2001). In order to isolate the contribution of such
effect, we quantify the degree of purity of the QD states, by
computing the linear entropy:
to evolve into a mixture, with
reduced coherences and nonzero occupancy of all levels. This limits
the maximum tangle that can be achieved as was described by
Munro et al. (2001). In order to isolate the contribution of such
effect, we quantify the degree of purity of the QD states, by
computing the linear entropy:
which is 0 for a pure state, and 1 for a maximally disordered state (where the four dot states have the same probability
![\includegraphics[width=0.6\linewidth]{chap6/fig_3.ps}](img1787.png) |
The entangling of the dots in the singlet state (rather than the
triplet) is a natural way to achieve a good degree of tangle and
purity at the same time, as in the limiting case where parameters for
each dot are identical (![]() ,
,
![]() ), the singlet
becomes a ``dark state''. In the case where
), the singlet
becomes a ``dark state''. In the case where
![]() , it is
also decoherence free [Lidar et al. (1998)], i.e., is not affected
by the decoherence introduced by the pump. When the limiting case is
only approached (
, it is
also decoherence free [Lidar et al. (1998)], i.e., is not affected
by the decoherence introduced by the pump. When the limiting case is
only approached (
![]() ),
),
![]() becomes coupled
to the triplet-subspace by a small effective coefficient
becomes coupled
to the triplet-subspace by a small effective coefficient ![]() (see Fig. 6.2), and the population can be trapped in the
singlet state (see below). As we already mentioned, equivalent
trapping mechanisms have been reported when interacting with a common
squeezed bath by Ficek & (2002) and Akram et al. (2000). Our
proposal for achieving a high value of the tangle is based on a slight
imbalance between the coupling strengths of the QDs, resulting in a
very high occupation of the singlet state.
(see Fig. 6.2), and the population can be trapped in the
singlet state (see below). As we already mentioned, equivalent
trapping mechanisms have been reported when interacting with a common
squeezed bath by Ficek & (2002) and Akram et al. (2000). Our
proposal for achieving a high value of the tangle is based on a slight
imbalance between the coupling strengths of the QDs, resulting in a
very high occupation of the singlet state.
In Fig. 6.4 we plot the mean number of photons and
the population of the singlet state (inset), for
![]() . The
first dot is in the strong coupling regime with the cavity (
. The
first dot is in the strong coupling regime with the cavity (
![]() ), whereas the second one goes from weak to strong coupling
regime as a function of
), whereas the second one goes from weak to strong coupling
regime as a function of ![]() . If the QDs are pumped independently
(red line), the photon number increases with
. If the QDs are pumped independently
(red line), the photon number increases with ![]() , until the maximum
is reached for
, until the maximum
is reached for ![]() . The presence of the second dot in strong
interaction with the cavity increases nonlinearly the emission (see
below).
. The presence of the second dot in strong
interaction with the cavity increases nonlinearly the emission (see
below).
![\includegraphics[width=0.56\linewidth]{chap6/fig_4.ps}](img1794.png) |
On the other hand, when the pump is common, a very different behavior
is observed (blue line in Fig. 6.4). First, for
![]() , the single-QD limit is not recovered, since the cross pumping
term
, the single-QD limit is not recovered, since the cross pumping
term
![]() creates an effective coupling between the QDs,
which induces correlation between their states even when no
cavity-induced coupling is present. The other striking difference
occurs for
creates an effective coupling between the QDs,
which induces correlation between their states even when no
cavity-induced coupling is present. The other striking difference
occurs for
![]() : the photon number decreases, while the
singlet population increases. Here,
: the photon number decreases, while the
singlet population increases. Here,
![]() , and the singlet
is almost decoupled from the dynamics (see Fig. 6.2 and
the above discussion). There is a slow flow of population into the
singlet state with zero photons, which also has a very long relaxation
time. In the specific case
, and the singlet
is almost decoupled from the dynamics (see Fig. 6.2 and
the above discussion). There is a slow flow of population into the
singlet state with zero photons, which also has a very long relaxation
time. In the specific case ![]() , there is an abrupt change of
the photon number, and the system turns into an effective three-level
system, as the singlet is optically dark.
, there is an abrupt change of
the photon number, and the system turns into an effective three-level
system, as the singlet is optically dark.
The strong differences between the emission of a system under independent or common pumping evidenced in Fig. 6.4 (especially when one of the dots is not coupled to the cavity or when they are coupled in a similar way) provide a simple experimental hint to discriminate them.
In the case where the only decay channel for the dot is the emission
into the cavity mode (![]() ), this behavior is singular (black in
Fig. 6.4). For finite
), this behavior is singular (black in
Fig. 6.4). For finite ![]() , the singularity is
replaced by an abrupt maximum. The occupation of state
, the singularity is
replaced by an abrupt maximum. The occupation of state
![]() is enhanced. However, this state being strongly
coupled with the other two triplet states, the purity is not high and
the tangle remains zero. Therefore, in order to increase
is enhanced. However, this state being strongly
coupled with the other two triplet states, the purity is not high and
the tangle remains zero. Therefore, in order to increase ![]() , we
seek the set of parameters that maximize the singlet occupation,
knowing that a moderate population of triplet states does not suffice
(Fig. 6.4). The best regime corresponds to small
, we
seek the set of parameters that maximize the singlet occupation,
knowing that a moderate population of triplet states does not suffice
(Fig. 6.4). The best regime corresponds to small
![]() , and large ratios
, and large ratios
![]() . Besides, in order to keep
at a minimum the excitations of radiant states in such a
configuration, the QDs must be detuned from the cavity mode. In turn,
because of this detuning which weakens the dynamics, the pumping must
be increased. Accordingly, we show the tangle
. Besides, in order to keep
at a minimum the excitations of radiant states in such a
configuration, the QDs must be detuned from the cavity mode. In turn,
because of this detuning which weakens the dynamics, the pumping must
be increased. Accordingly, we show the tangle ![]() for
for
![]() ,
,
![]() ,
,
![]() , as a function of the
pumping
, as a function of the
pumping
![]() (Fig. 6.5). Larger
detunings increase the tangle, though this requires larger values of
the pump as well. For very high values of the pump, the emission from
the two dots gets quenched and the number of cavity photons vanishes.
The population saturates between the states
(Fig. 6.5). Larger
detunings increase the tangle, though this requires larger values of
the pump as well. For very high values of the pump, the emission from
the two dots gets quenched and the number of cavity photons vanishes.
The population saturates between the states
![]() and
and
![]() (with zero photon) and the tangle gets
spoiled. There is therefore a maximum for a given detuning, as shown
on Fig. 6.5 from the numerical results.
(with zero photon) and the tangle gets
spoiled. There is therefore a maximum for a given detuning, as shown
on Fig. 6.5 from the numerical results.
![\includegraphics[width=0.5\linewidth]{chap6/fig_5a.eps}](img1806.png)
![\includegraphics[width=0.5\linewidth]{chap6/fig_5b.eps}](img1807.png)
![\includegraphics[width=0.5\linewidth]{chap6/fig_5c.eps}](img1808.png)
![\includegraphics[width=0.5\linewidth]{chap6/fig_5d.eps}](img1809.png) |
In the following we consider a detuning
![]() between the dots
and the cavity mode, so as to keep realistic values of the pump
required to maximize the tangle, namely,
between the dots
and the cavity mode, so as to keep realistic values of the pump
required to maximize the tangle, namely,
![]() as
read from the magenta line in Fig. 6.5. In
Fig. 6.6, we make a systematic analysis of the steady
state in terms of (a) its cavity population, (b) population of the
singlet state with zero photon
as
read from the magenta line in Fig. 6.5. In
Fig. 6.6, we make a systematic analysis of the steady
state in terms of (a) its cavity population, (b) population of the
singlet state with zero photon
![]() (almost equal to
the total population of the singlet), (c) tangle and (d) entropy, by
scanning the space of relevant parameters
(almost equal to
the total population of the singlet), (c) tangle and (d) entropy, by
scanning the space of relevant parameters ![]() and
and
![]() ,
(in units of
,
(in units of ![]() ) and keeping other parameters fixed to the values
given above. The maximum of the tangle (
) and keeping other parameters fixed to the values
given above. The maximum of the tangle (![]() , marked with a
cross), is achieved at
, marked with a
cross), is achieved at
![]() and
and
![]() (see
Fig. 6.5). It corresponds to the minimum entropy and
an increase of the population of the state
(see
Fig. 6.5). It corresponds to the minimum entropy and
an increase of the population of the state
![]() , and
therefore to a decrease of
, and
therefore to a decrease of
![]() .
.
Entanglement between the QD excited states is not an easy magnitude to access experimentally (other than by reconstructing the QD density matrix with quantum tomography). The low number of cavity photons associated with the maximum of the tangle, and consequently the low cavity emission, can be used as an experimental indication of a high degree of entanglement.
![\includegraphics[width=0.7\linewidth]{chap6/fig_6.ps}](img1819.png) |
Another important feature of these plots (Fig. 6.6) is
that they are not symmetric with respect to ![]() and in this
case, it is easier to reach the maximum tangle when the second dot
coupling is smaller than the first. The sign of
and in this
case, it is easier to reach the maximum tangle when the second dot
coupling is smaller than the first. The sign of ![]() which
maximizes the tangle for a given
which
maximizes the tangle for a given ![]() depends on the position
of the maxima in the curves of
depends on the position
of the maxima in the curves of
![]() and singlet population with
respect to
and singlet population with
respect to ![]() around the singularity
around the singularity ![]() . The best case is
the one which maximizes the singlet population and minimizes the total
population.
. The best case is
the one which maximizes the singlet population and minimizes the total
population.
In Fig. 6.7--the counterpart of
Fig. 6.4 in the configuration under consideration,
which is suitable for entanglement--these maxima are obtained
for ![]() . Note that in Fig. 6.4 the situation
is opposite. Note also that a very strong coupling of the QDs with the
cavity is not needed neither. Fig. 6.7 shows as well the
transition from the common bath (
. Note that in Fig. 6.4 the situation
is opposite. Note also that a very strong coupling of the QDs with the
cavity is not needed neither. Fig. 6.7 shows as well the
transition from the common bath (![]() ) to independent ones (
) to independent ones (![]() ),
in the case where the total pump is fixed
),
in the case where the total pump is fixed
![]() . It gives an idea of the
overlap needed to obtain a sizeable tangle. No tangle is obtained for
an overlap less than 66%. The important overlap which is required can
be obtained experimentally by application of an electric field which
can squeeze the areas of two nearby QDs into each other.
. It gives an idea of the
overlap needed to obtain a sizeable tangle. No tangle is obtained for
an overlap less than 66%. The important overlap which is required can
be obtained experimentally by application of an electric field which
can squeeze the areas of two nearby QDs into each other.
Elena del Valle ©2009-2010-2011-2012.


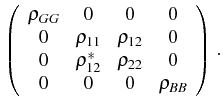
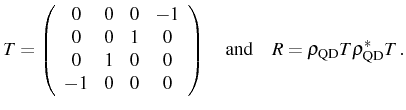
![$\displaystyle S_L=\frac{4}{3}[1 - \Tr{( \rho_\mathrm{QD}^2)}]=\frac{4}{3}[1 - \...
...G}^2 +\rho_{11}^2 +\rho_{22}^2 + \rho_{BB}^2 + 2\vert\rho_{12}\vert^2 \big)]\,,$](img1777.png)