The Bohr model

(Part of the Wolverhampton Lectures of Physics's Quantum Physics Course)

On sait quelle a été la magnifique fortune de la théorie de Bohr depuis dix ans [...] Mais la signification profonde des quanta est restée inconnue. [...] Le moment semblait venu de tenter un effort dans le but d’unifier les points de vue corpusculaire et ondulatoire et d’approfondir un peu le sens véritable des quanta.

—Louis de Broglie.

Spectroscopists in the late 19th century discovered that the radiation from hydrogen consisted of spectral lines, i.e., the emission occurs at precise frequencies.

Empirically, it was found (by Rydberg) that the lines occurred at wavelengths given by the difference of the inverse square of integers:

$${\displaystyle {\frac{1}{\lambda}}=R_{\text{H}}\left({\frac{1}{n_{1}^{2}}}-{\frac {1}{n_{2}^{2}}}\right),}$$

with $R_\text{H}$ the Rydberg constant. As such, the situation was tantamount to pre-Newtonian Physics where Kepler's laws of planetary motion were providing working rules to describe the observed phenomenology but with no justification as to their origin or underlying mechanism. The hydrogenoid motion was awaiting its Newton counterpart to provide the fundamental theory. The main hurdle to those who attempted such a derivation based on the Rutherford picture of an electron bound to a small-size nucleus, was rooted in the fact that an electron in a circular orbit accelerates (albeit it does not need to change its speed, it changes its velocity) and according to the most successful theory of the time, electrodynamics, which was successful in explaining the color of the sky and of its rainbows (no small feasts), an accelerating charge radiates. Not only was this predicting a continuous spectrum of emission, but also calculations showed that the lifetime of an electron in this context is extremely short. All this was against the observed stability of hydrogen and its discrete spectrum of emission. A radically new theory was needed and this was brought forward by Niels Bohr whose insights were so close to the actual picture that his model is nowadays denominated, along with other similar tricks or heuristic findings, as the "old quantum theory".

Bohr was looking for a physical picture that would constrain the motion on orbits of fixed radii, with no possibility to spiral inward the nucleus as a result of dissipating energy. The existence of particular orbits would then explain the discrete set of spectral lines. He, therefore, cut the Gordian knot by postulating it! Namely, he imposed the quantization of the angular momentum $L=mvr$ (with $v$ the speed of the electron orbiting at a distance $r$ from the nucleus) into integer multiples of Planck's constant $\hbar$ (we remind that $\hbar\equiv h/(2\pi)$ and $p=mv$):

$${mvr}=n\hbar\tag{1}\,.$$

In this equation, $n=1, 2, \ldots$ is an integer called the principal quantum number. Bohr thus settled for the following postulates, having already solved the problem of the stability of hydrogen:

1. The electron moves in circular orbits around the atom.
2. The orbit is such that the angular momentum of the electron is quantized (in units of Planck's constant $\hbar$).
3. The electron can change orbits, by jumping from one to the other, releasing or acquiring the energy difference in the process.

The proof for the validity of these postulates is that they allow to derive the main results of hydrogen's spectroscopy, and, compellingly, to link its empirically derived constant to many of the most important fundamental constants of nature. This is achieved as follows. For an electron of mass $m$ and charge $-e$ (opposite as the proton so their product is $-e^2$), and moving in a circular orbit of radius $r$ in Coulomb's potential $V=-e^2/(4\pi\epsilon_0 r)$, Newton's second law $F=ma$ gives:

$${e^2\over 4\pi\epsilon_0 r^2}={mv^2\over r}\tag{2}$$

since $a=v^2/r$ for a central force, with $v$ the speed of the electron, and $F=-|\nabla V|$.

Equations (1) and (2) make two equations for two unknown $r$ and $v$, which can be easily solved:

$$\begin{align} r&=n^2a_\mathrm{B}\,,\\ v&=\alpha c/n\,, \end{align}$$

where we have defined the Bohr radius (with units of distance):

$$\boxed{\displaystyle a_\mathrm{B}\equiv{4\pi\epsilon_0\hbar^2\over me^2}}$$

and the fine-structure constant (which has no dimension and includes the speed of light $c$ so that $v$ can be related to a fundamental constant of speed):

$$\boxed{\displaystyle\alpha\equiv{1\over4\pi\epsilon_0}{e^2\over \hbar c}\approx{1\over 137}}$$

The measured value of the fine-structure constant is $\alpha^{−1}=137.035999173(35)$ (uncertainty in parentheses) with a great agreement to the theoretical value. The small value of this parameter is the basis for the standard model of elementary particles as it allows a perturbative treatment in terms of a series of processes whose $n$th order is weighted by $\alpha^n$. It also shows, since the speed of the electron is $v=\alpha c$, that relativistic effects can be neglected in a first approximation. If we compute the energy as kinetic $K$ (${}=\frac12mv^2$) plus potential $V$ (Coulomb), we find:

$$E={e^2\over 8\pi\epsilon_0r}-{e^2\over4\pi\epsilon_0 r}=-{e^2\over8\pi\epsilon_0r}$$

(where we used (2) again for the kinetic energy). Substituting the radius $r=n^2a_\mathrm{B}$ in this result yields

$$\boxed{\displaystyle E_n={E_1\over n^2}}$$

where

$$E_1=-{m\over2\hbar^2}\left({e^2\over4\pi\epsilon_0}\right)^2=-{mc^2\alpha^2\over2}\approx-13.6\text{[eV]}$$

This is an important constant that is related to Rydberg's constant and was known already at the time to be the ionization energy of Hydrogen. The 3rd Bohr postulate thus explains the discrete set of spectral lines from a transition between an initial $i$ and final state $f$ that yields an energy for the emitted photon $E_\gamma=E_i-E_f$:

$$E_\gamma=E_1\left({1\over n_f^2}-{1\over n_i^2}\right)$$

and from Planck's formula $E_\gamma=h\nu$ relating energy and frequency, one can finally derive Rydberg's formula for the wavelengths $\lambda=c/\nu$ of the hydrogen spectrum. The underlying mechanism is thus captured in this picture:

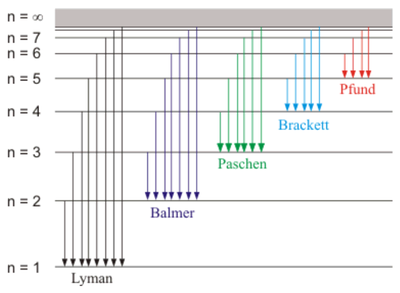
So with these simple arguments and manipulations, Bohr was clearly onto something.

A convincing and appealing hypothesis to explain Bohr's quantization of angular momentum was later proposed by de Broglie's wave theory of matter, which states that the momentum of a particle $p$ can be related to a wave with the corresponding wavelength. This was motivated, foremost, not by Bohr's model, but by de Broglie's admiration for Einstein's works. Einstein had previously restored (in 1905) the particle-status of light, one of the major coup-de-théâtre of Science after the compelling evidence to rule out Newton's corpuscular theory of light in favor of a wave interpretation. Although most people were not taking this idea too seriously (it had to wait Compton's 1923 experiment demonstrating a single-photon recoil by a particle-particle scattering process), de Broglie was. Einstein had made this bold move to account for the photoelectric effect, for which he eventually won the Nobel prize, although his theory of relativity was a much bigger achievement. But the nature of space and time was even more controversial than the corpuscular interpretation of light and relativity was swept under the Nobel rug as "other services to theoretical physics". De Broglie had been impacted by both relativity and the corpuscular theory of light. Special relativity shows that mass is a so-called relativistic invariant and relates the time-part ($E/c$) of the quadrimomentum to its space-part $p$ as $(mc)^2=(E/c)^2-p^2$, so that, solving for the energy:

$$E=\sqrt{p^2c^2+m^2c^4}$$

For a zero-mass particle, like the photon, therefore, $E=pc$. That's the relativistic aspect. The photoelectric aspect brings the relation $E=h\nu$ and equating these leads to $pc=hc/\lambda$ or:

$$\lambda={h\over p}\,.$$

This holds for photons (which indeed have zero mass), but de Broglie generalized this relation to matter by postulating (in 1924) that all matter was exhibiting wave phenomena, but with a wavelength so small for macroscopic objects that this could be disregarded. De Broglie thus justified Bohr's quantization of angular momentum by standing waves: the electron circling around the nucleus at a radius $r$ has to satisfy $2\pi r=n\lambda$ or, using De Broglie's wavelength $2\pi r=nh/(mv)$ which is Bohr's starting point Eq. (1).

De Broglie's prediction was a posteriori not really so convincing. It was further confirmed by the Davisson-Germer experiment (1927) who observed the diffraction pattern of electrons from a surface of nickel (they were initially studying the surface of nickel but after seeing some of their results displayed by Born in support of de Broglie's theory they turned to the more fundamental aspect of wave-particle duality and eventually got the Nobel prize for the confirmation that electrons can behave as waves). De Broglie had started a new field in physics, the "mécanique ondulatoire" (wave mechanics). He submitted his thesis to Langevin who was not sure whether this was a breakthrough or unjustified speculations and lucky guesses, and he passed the work to Einstein, who on the opposite expressed his strong support for the work and referred to it (for instance in his theory of Bose-Einstein condensation), which popularized the work to Schrödinger and others. Schrödinger eventually formulated a complete dynamical theory for the wave evolution, resulting in Schrödinger's equation. In his first paper on this topic, he credits de Broglie's input in these terms:

Above all, I wish to mention that I was led to these deliberations in the first place by the suggestive papers of M. Louis de Broglie, and by reflecting over the space distribution of those "phase waves", of which he has shown that there is always a whole number, measured along the path, present on each period or quasi-period of the electron.

He then proceeds to point at differences of interpretations, which remained, nevertheless, a point of dispute between them and is still one of the most troubling aspects of the theory nowadays. De Broglie favored a pilot-wave interpretation, where the wave guides the electron:

that the particle must be the seat of an internal periodic movement and that it must move in a wave in order to remain in phase with it was ignored by the actual physicists [who are] wrong to consider a wave propagation without localization of the particle, which was quite contrary to my original ideas.

Such a pilot-wave idea was later developed by David Bohm and constitutes one of today's contenders for the interpretation of quantum mechanics, albeit not the most popular one. Regardless of what the wavefunction is, we will see in the next Lecture how it supplements Bohr's old theory of the atom.

Links

• De Broglie's thesis (French).
• De Broglie’s thesis: A critical retrospective.
• Electron diffraction: fifty years ago (written in 1978, so 96 ago).
• Revisiting Louis de Broglie's famous 1924 paper in the Philosophical Magazine.
• Critical Appraisal of Physical Science as a Human Enterprise, with interesting chapters on de Broglie (including on his reputation).
• Classical Lifetime of a Bohr Atom by Kirk McDonald.
• Further readings: Bohr's paper