Deterministic entangling gates with nonlinear quantum photonic interferometers. F. Scala, D. Nigro and D. Gerace in Commun. Phys. 7:118 (2024). What the paper says!?

The Authors report that machine-optimizing dual-rail qubit encoding with "interacting photons" (which the Authors prefer to polaritons), i.e., bosons with Kerr-type nonlinearities, combined to phase-shift from tunneling between rails, they can design CNOT and Molmer-Sorensen two-qubit gates with arbitrary high (close to 1) fidelities.

Their Hamiltonian:
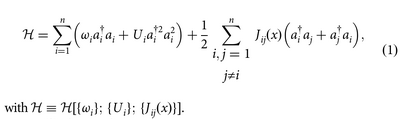
(I'm not sure the line below clarifies anything). It is used with $n=4$ to implement a CNOT and Molmer-Sorensen gate.
The mere fact that this is at all possible is a great result, and possibly a breakthrough towards implementation of a working quantum computer. They say Ref. [1] implements a similar scheme (just not observing loss of efficiency for too strong interactions, which is what I'd have expected).
This expands the work of Nigro et al.[2] which describes interferometers of interacting photons in single-rail encoding, so with the difficulty of measuring no photon as one of the basis states. Regardless, dual-rail encoding is apparently better for bosons:
photon bunching has been shown to severely hinder the application of single-rail encoding for optical quantum
computing
They do not provide (at least not in the main text) the actual parameters that implement the gates, just the fidelity for a given number of blocks. They also do not discuss much the underlying reason why weak nonlinearities would result in such strong deterministic control of the states. They do not consider actually entangled states, but since their scheme is (shuold be) linear at the interacting-Hamiltonian level (no factorization of correlators), this should indeed work as a fully-fledged quantum gate.