
This page is still in progress.Near-100% two-photon-like coincidence-visibility dip with classical light and the role of complementarity. S. Sadana, D. Ghosh, K. Joarder, A. Lakshmi, B. Sanders and U. Sinha in Phys. Rev. A 100:013839 (2019). What the paper says!?

This paper makes the point with the standard HOM effect that I (independently, but later) made with spatial correlations of vortices, that coherent states have no correlations and that fake "quantum correlations" can be produced by tweaking the coherent state phases. In their case, they show that averaging over 0 and $\pi$ relative phase, they get 100% HOM dip with laser light. This is resolved by introducing the distinction between quantum and statistical averages.
This is a nice paper that should be studied in full depth.
They compute with semiclassical theory the coincidence probability as:
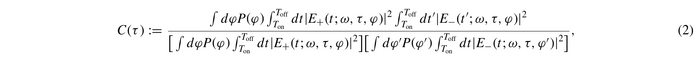
and if time windows are large enough, they find this is simply:
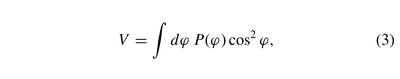
from what they observe that if the phase is randomly chosen to be 0 or $\pi$, then the visilibity of the HOM dip is: $$V=1$$
They touch upon the complementary principle («Contraria sunt complementa»).
There is a clear discussion (with examples) of the criterion that the dip shouldn't be less than 50% for classical light:
Despite the immense importance, applicability, and suc cess of HOM TPCVD, a widespread misconception is that exceeding a 50% TPCVD falsifies classical electromagnetic field theory. Example quotations include “fourth-order inter ference of classical fields cannot yield visibility larger than 50%” [11], “as long as the visibility of the coincidence dip is greater than 50%, no semiclassical field theory can account for the observed interference” [9], “visibility, being greater than 50%, is clear evidence of non-classical interference” [12], and “classical theory of the coherent superposition of electro magnetic waves, however, can only explain a HOM dip with V ⩽ 0.5” [13]. This myth matters as the 50% dip threshold is widely accepted as proving that two-photon interferometry has entered the quantum domain.
and again
The 50% TPCVD is believed to be the threshold between classical and quantum behavior of light, because independent classical pulses with uniformly randomized relative phase yield V = 1/2 [13,14]. The argument against the classical de scription is that it fails to predict the observed 100% visibility and, instead, puts an upper bound of 50% on it.
and again
if the phase between the input signals is randomized over a preselected set, 100% visibility can be achieved even with classical pulses.
They refer to [1] instead of depth of the dip for «real quantum signature».