Stimulated emission of a microcavity dressed exciton and suppression of phonon scattering. S. Pau, G. Björk, J. Jacobson, H. Cao and Y. Yamamoto in Phys. Rev. B 51:7090 (1995). What the paper says!?

This is an early work on the relaxation of polaritons according to rate equations, with fairly extensive details on the microscopic Hamiltonian (scattering rates), derivation of the rate equation itself, its numerical solution and comparison to experiments.
This is all driven by phonon scattering, with no polariton-polariton interactions.
They have three polariton branches: «the upper transverse, the lower transverse, and the longitudinal polariton branch, respectively. The longitudinal branch is not optically active but can be excited by scattering processes.»
They provide fairly extensive details (and literature from bulk polaritons) on the scattering rates.
The rate equations are derived from Heisenberg equations and reach the form:
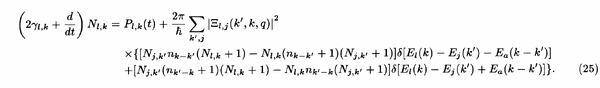
with $N$ for polaritons and $n$ for phonons, that are taken from the Bose-Einstein distribution.
They solve it numerically for the three branches and find, for the lowest-branch population, presented as a function of the angle rather than momentum with

They describe this figure briefly (especially compared to the rest of discussions on microscopic details) as follows:
At low pump intensity, the majority of the polaritons are cen tered at the pump wave vector. As the pump increases, the polariton population is scattered to the $k_\parallel=0$ state due to its coupling to the phonon bath. The net result is a buildup of polariton population at $k_\parallel=0$, which is analogous to the bottleneck effect of the bulk polariton.
Then they proceed to make a physical toy-model of this process:

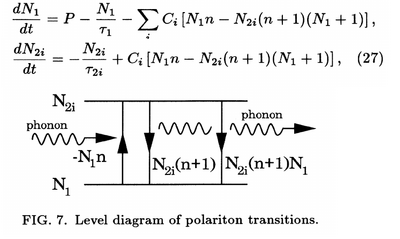
where initially «the sum is taken over all modes i» but quickly they group all i modes into «an effective polariton population $N_2\equiv\sum_iN_{2i}$» and solve for this simple system, arriving to:
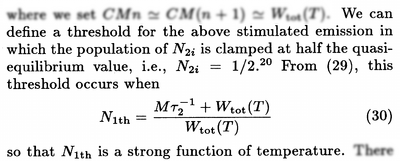
where the $N_{2i}=1/2$ is a bit unclear (as it concerns all the other modes). This seems to be a saturation criterion. In their footnote 20 they further comment:
If the stimulated emission term is taken into account, then there is a possibility of population buildup for the $k\neq0$ 0 polariton. In this case, the natural definition of lasing threshold is the point where $N_{2i}=n$, i.e. , when the $k\neq0$ polariton has the same population as the population of the phonon bath.
From this they compute, apparently essentially analytically, a fairly cryptic quantity based on what they call the quantum efficiency and differential quantum efficiency, defined as:
At 4 K, the differential quantum efficiency is independent of pump rate and is equal to one (P = I, thresholdless behavior).
The meaning of this quantity or the one they actually consider, which is «the normalized differential quantum efficiency» $${P\over N_1}{dN_1\over dP}$$ is a bit unclear but the simple model (Fig. 8) agrees well with the measurement (Fig. 9):
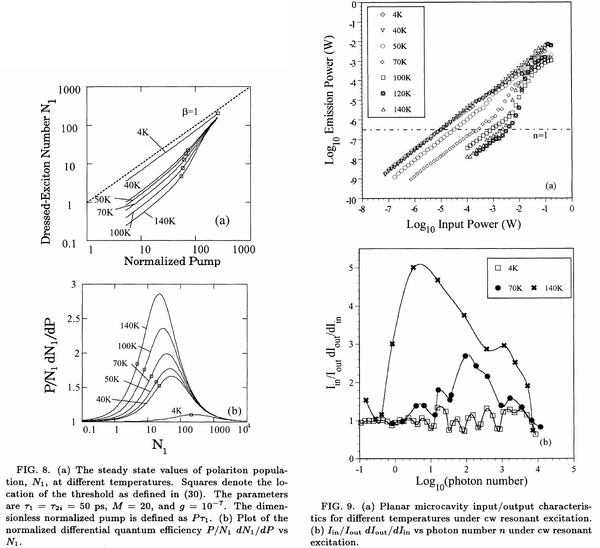
and they describe this in the experimental part (not the theory one), although this clarifies little more. They arrive to the conclusion that the mechanism of "lasing" or population buildup is different from a standard laser as the threshold is temperature dependent.
Interestingly, in line with Weisbuch's initial reluctance to call his effect a "polariton",[1] here they refer to "dressed excitons" which they justify with the lack of propagation:
The term dressed exciton is used for the $k_\parallel=0$ polariton in analogy to the dressed atom in atomic cavity quantum electrodynamic. We use this nomenclature for the spatially stationary polariton because the polariton concept is often associated with propagating waves and the $k_\parallel=0$ polariton does not propagate.
I am not sure I understand what they mean here: (should be "also coupled to a single photon mode at all k" to realize strong coupling)
The 2D excitons with $k_\parallel\neq0$ also couple to a contin uum of microcavity photon modes which have net prop agation along the quantum-well plane, leading to a prop agating microcavity polariton.