«this topic appears to have been forgotten in the past few years.»

Explanation of the quantum phenomenon of off-resonant cavity-mode emission. S. Echeverri-Arteaga, H. Vinck-Posada and E. Gómez in Phys. Rev. A 97:043815 (2018).  What the paper says!?

This is an interesting, but to me, mysterious paper, as it has been written at the same time as we had a similar activities with the Authors with similar interpretations which they did not relate together! I had to discover this and the related Ref.  from an experimental paper.

Here they deal with the simple Jaynes-Cummings model, to which they add the dissipative coupling $\mathcal{L}_{\sigma^\dagger a}$:

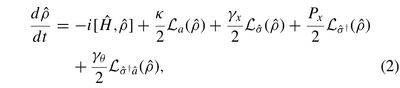
This results in an additional peak:

clarifies the existence of the central peak as a signature of the coexistence of the doublet phase

as well as the singlet phase in the system.

which they say explains K. Hennessy's triplet,

an extraordinary experiment in

the strong-coupling regime with exceptional results

for which

we demonstrate that the spectral triplet that has been observed experimentally is a consequence of a dynamical

phase transition in the system.

They make some interesting points, although I am unsure how much of them are fully correct, starting with the fact that Hennessy's observation is pretty well explained by the cavity-feeding mechanism, although their Lindblad form could capture that as well or better or even simplify the same mechanism.

The physics is the most interesting.

The Liouvillian retains the nice properties of the JC model:

They bring attention to Ref.  and make interesting comments following their Eq. (3) on exact diagonalization of $\mathcal{L}$ vs imaginary parts in the Hamiltonian.

They make a decomposition of the Liouvillian in $4\times4$ subgroups thanks to the above conservation of excitations:

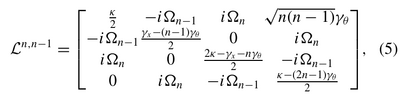
and make a key observation:

Therefore, it is expected that any significant information about the emission properties

of the system comes from this subspace.

This seems to be closely related to our dephasing of nonlinear transitions in the Jaynes-Cummings model. They cite it (the only paper of mine they cite) but do not usefully comment on it and such connections.

They make interesting connections to exceptional points (which we didn't, not knowing about them back then):

These critical values are exceptional points (EPs) since they are related to the coalescence of two eigenvalues $\lambda^{n,n-1}_{-,\pm}$ and the

−±dimension of the subspace drops by 1.

They also do not cite our related work without their new term, although they refer to the dissipative Jaynes-Cumming ladder, which I believe is first introduced there.

They find this interesting relationship between linewidths:

whose exact meaning remains unclear on first reading, but it seems to be important:

In other words, when Eq. (6) is not valid, a structural

change occurs in the emission properties of the nth subspace.

Then they have a quite fascinating discussion on how this constitutes a dynamical phase transition, but this should be studied in more details to opinate stronger. I still remain flabbergasted that they didn't mention this work to us!