Suppression of the bottleneck in semiconductor microcavities. T. Doan and D. T. Thoai in Solid State Commun. 123:427 (2002).  What the paper says!?

«we expect our results remain qualitatively valid

even in a better treatment of polariton relaxation kinetics»

This is an early Boltzmann equations treatment of polariton BEC which claims that the bottleneck can be overcome with phonon relaxation only.

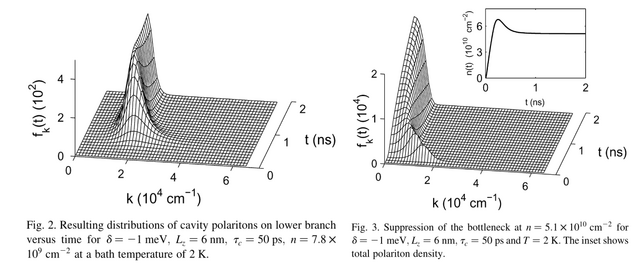
They basically find that by pumping enough, they go from seeing the bottleneck (Fig. 2, left) to overcoming it and condensing at $k=0$ (Fig. 3, right):

Their rate equation (along with scattering terms below):

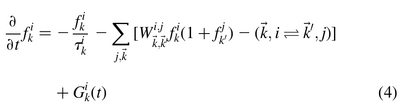
with also rather unnecessary abrupt changes for decay rates as opposed to polariton lifetimes from Hopfield coefficients:

They find that similar attempts in the bulk with steeper dispersion relation does not vainquish the bottleneck:

The main difference in the dispersion relation between cavity polaritons and bulk polaritons is the slope of E(k) versus k in the bottleneck k-region. The very high value of the slope of the bulk polaritons (70 times higher than the slope of the cavity polaritons) is very unfavorable for the

suppression of the bottleneck even at very high densities.

It could be that the simulation of this very early model is too simplistic, or just wrong, as consensus and later analyses seem to be that phonons alone do not overcome the bottleneck. The Authors relate their work to A. Tartakovskii et al.'s observation of collapse of the bottleneck, which these Authors, however, attribute to polariton interactions, not the phonon mechanism alone at higher pumping.

The good reference for their Eq. (1) is Savona et al.