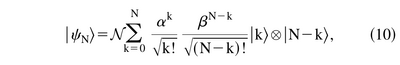«It does not matter whether coherences exist or not; observable phenomena in optics and quantum optics are unchanged, and in this way optical coherences may be regarded as a convenient fiction.»

Optical coherence: A convenient fiction. K. Molmer in Phys. Rev. A 55:3195 (1997).  What the paper says!?

This page is among our 'okay articles'. It should be further expanded but we hope that it will still be useful in its present stage.

This is an interesting paper that questions whether the phase $\operatorname{Arg}(\alpha)$ exists in $\ket{\alpha}$ or if this is is just a mathematical convenience for some information encoded at a more involved level, with entanglement to other modes.

the field amplitudes are replaced by quantum operators, and it is the vanishing of their expectation values that is the topic of this paper.

That $\langle a\rangle$ is truly zero would appear to have consequences:

If there are no mean fields, there is no mean polarization induced in media illuminated by the light field, and the clas sical theory of light is not merely a ‘‘theory of mean values’’ of the quantum theory. Large parts of optics and of atomic physics, e.g., the theory of dielectrics, the coupled Maxwell Bloch equations, and the role of atomic coherences, should in principle be reexamined to verify that predictions based on postulated mean amplitudes can also be obtained more rig orously.

Interesting comment on atom-photon correspondence:

Atoms, unlike photons, are not created or annihilated in experiments, but a conclusion of the present paper is that this is not a fundamental difference between, e.g., a laser and a coherent source of bosonic at oms. In turn, the validity of many-body physics concepts such as spontaneous symmetry breaking might be examined along the same lines as the ones applied here for optics.

Problem of the seed:

Hence, if all such quantities have vanishing mean values at some initial time, they will never develop nonvanishing expectation values.

Can be solved by turning to autocorrelators who, at $t=0$, are non-vanishing:

This is thanks to the quantum regression theorem:

From a formal perspective, one- and two-time expectation values obey the same set of equations, merely with different initial conditions.

Appearance of the $c$-numbers:

It is not only conve nient, it is absolutely necessary to break this hierarchy of entanglement as close as possible to the target system of interest, and this is what we do when we replace field opera tors by c numbers.

On what I call quantum and statistical average:

The idea of associating pure states with density matrix problems has attracted much interest. For dissipative prob lems of a very wide class, it has been shown that one may consistently evolve an ensemble of wave functions, so that they, on the average, reproduce the reduced density matrix for the system. These approaches have been described by the names ‘‘quantum trajectories’’ [2], ‘‘Monte Carlo wave functions’’ [3], ‘‘quantum state diffusion,’’ and ‘‘decoherent histories’’ [4]. The state vectors can be ascribed physical meaning as the states conditioned on certain measurements performed on the surroundings of the system.

Then he connects the optical observables to condensed-matter concepts, such as ODLRO.

On symmetry breaking:

Rather than deal with spontaneous symmetry breaking in our exact quantum optics systems, we may refer to the mean field approximations as ‘‘symmetry-breaking approxima tions.’’ The system and the interactions are simply replaced by something different which ~i! is easier to deal with for mally and conceptually and which ~ii! yields nearly the same results as the more cumbersome exact approach, if such an approach within the symmetry conserving framework is fea sible at all.

An interesting comment on coherent states as "pointer states" in their resilience «being acted upon by any linear combination of the annihilation operators of the two oscillators», apparently always going $\ket{\psi_{N-1}}$ (check this):