Quantum coherence of a long-lifetime exciton-polariton condensate. Y. Brune, E. Rozas, K. West, K. Baldwin, L. Pfeiffer, J. Beaumariage, H. Alnatah, D. Snoke and M. Aßmann in Commun. Mater. 6:123 (2025).  What the paper says!?

The authors study polariton condensate buildup, and report the interesting following experimental data:

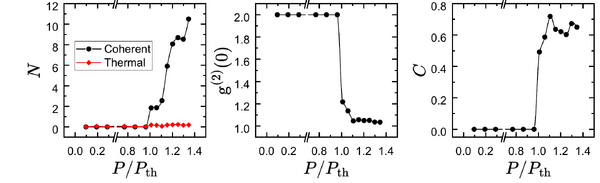
From the conceptual point of view, this is an extension of their previous work by C. Lüders et al., on quantum coherence, where they now «optimize the quantum coherence of a nonresonantly excited exciton-polariton condensate of long living polaritons by minimizing the condensate’s interaction with the surrounding reservoir of excitons and free carriers». They upgrade $\mathcal{C}\approx 0.21$ to well above 0.6 as can be seen above. They attribute this to long lifetime and thus thermalization and an evidence that the exciton reservoir does not destry "quantum coherence".

The reservoir technique is the same as in other papers:

We spatially separate the polariton condensate from the surrounding incoherent carrier reservoir, minimizing the interaction between them

where it is known to enhance other observables:

In terms of g(1), it has already been demonstrated that this method improves the condensate’s spatial 28 and temporal29,30 coherence.

Same statements as in the previous paper, in particular:

Polariton condensates may carry quan tum superpositions in the Fock basis, which can either be directly exploited as a resource or transferred into quantum entanglement or other non classical correlations^19,20.

Like before, they do not measure the actual phase but infer it is there:

Experimentally, the density matrix can be reconstructed using quantum state tomography. However, this requires a temporally stable phase between the local oscillator (LO) and the signal, a condition not satisfied in polariton condensates. We circumvent this obstacle by assuming that the polariton condensate is in a single mode Gaussian state in the absence of squeezing, and can thereby, be described as a displaced thermal state with both coherent and thermal components.

They measure instead the phase averaged Husimi Q distribution:

we measure the phase averaged Husimi-Q distribution in phase space, which provides equivalent information. The Husimi-Q distribution is well-defined for states near the vacuum, and its positivity and smoothness allow it to be accessed experimentally.

They have an interesting short paragraph on the role of the dark-exciton reservoir:

a non-negligible number of dark excitons accumulates inside the center of the ring and interacts with the condensate

they provide a constant (non-fluctuating) background potential, which doesn't spoil coherence.

The drop in $g^{(2)}$ is not simultaneous with population buildup (as predicted by Shishkov):

Although we do not observe any more jumps in the photon number for this pump power, g(2)⁽⁰⁾ does not decrease yet, probably due to the fact that condensed polaritons still exhibit some thermal characteristics, as the power is not sufficiently far away from the threshold.

Some mechanical noise at high power affects population but not $g^{(2)}$.

This comment is strange (as if they don't actually measure $g^{(2)}$ of 2 but infer it from previous measurements):

Below the condensation threshold, our estimated g(2)⁽⁰⁾ consistently exhibits a value of 2. We want to emphasize that our fitting method provides this value for a vacuum state and the uncondensed lower polariton branch does not overlap with the local oscillator. Nevertheless, previous works have exhaustively demonstrated that polaritons below the condensation threshold are generally characterized by a thermal state with g(2)(0) = 2.

They attribute higher "quantum coherence" in this case thanks to longer lifetime and thus better thermalization. Regarding the role of the reservoir, they comment:

increasing the polariton lifetime to bring the polariton condensate closer to a thermalized equilibrium state is significantly more beneficial to its quantum coherence properties than just separating it from incoherent reservoirs.

It's not clear why they assume interactions or even a potential would spoil their "quantum coherence", as it wouldn't per se make it less of a pure state (superposition), just one which is not the displaced thermal state. This shows again how fragile is their assumption.