Analytical framework for non-equilibrium phase transition to Bose–Einstein condensate. V. Yu. Shishkov, E. S. Andrianov and Yu. E. Lozovik in Quantum 6:719 (2022).  What the paper says!?

This page is among our 'okay articles'. It should be further expanded but we hope that it will still be useful in its present stage.

This is a little jewel, that studies the ideal (non-interacting) bose gas' dynamics, in particular its Bose-Einstein condensation.

Their most important results, first for the microcanonical [closed-system] case with exactly $N$ particles:

• The fraction of condensed particles in 2D and 3D, which they say recover textbook results in the limits $N,V\to\infty$, $N/V=cst$ (check with Ref. ). In 2D, this is never a finite number (indeed this is a negative number so interpretation of this formula should be more careful; see Fig. 1(a) for finite N):

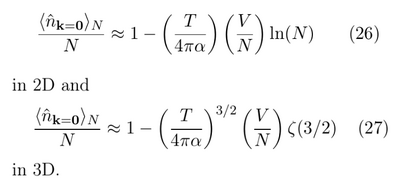
Here $\alpha$ is the factor in the dispersion (so basically the inverse mass).

• The coherence length and decay of first-order correlation function below treshold:

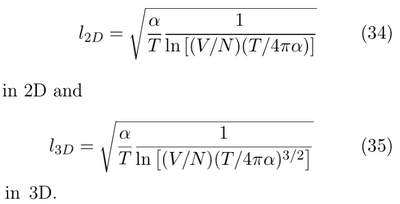
and

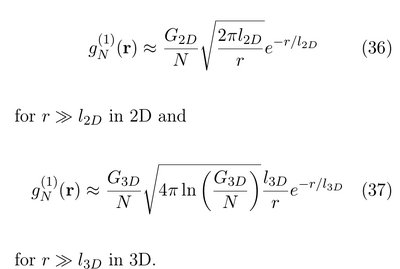
• They also provide above-threshold results (Eqs. (32-33)) where there is a plateau (ODLRO) which is finite even in 2D for finite N (unclear though where dimensions enter these formulas).
• Linewidth of the ground-state (annoying notation $\Delta\omega_{\mathbf{k}=\mathbf{0}}$) showing that in 2D, line-narrowing doesn't follow the Schawlow-Townes formula:

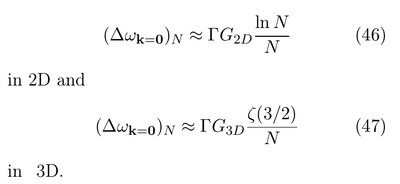
• The two-photon correlation function for the ground state is $1-1/N$ when there is condensation (of a Fock state, due to their microcanonical approach), and $\approx2$ otherwise (thermal state, even though, again, the total number of particles is fixed). When the condensate builds up, the $g^{(2)}$ gets close to 1 but from above:

Then when they turn to the open system, or with not-exactly conserved $N$, they :

This work extends to infinite size system (and continuous ones) results from a previous paper which they describe as follows:

Relying on similar ideas, recently, it has been shown that, in the case of fast thermalization of polaritons, the density matrix can be obtained analytically for arbitrary finite sets of polariton states [35].

(the similar ideas are from my earlier toy-model) And the problems this pauses:

However, due to the finiteness of the states, this approach is limited in its ability to analytically investigate the influence of the po laritons’ dispersion and dimension on the conden sation threshold, buildup of coherence, long-rage spatial correlations, and linewidth.

They rely on one main assumption:

At the first step, it is assumed that in each sector of Fock space with fixed particle number N distributed in the whole system, the density matrix $\rho_N$ is in thermal equilibrium.

Although this doesn't seem entirely innocuous, they observe that «this assumption is fulfilled if thermalizing processes are much faster than processes that change the particle number (external pumping and dissipation)». The approximation and procedure is detailed in Section 3.

Their technique then is to compute the density matrix for a fixed number $N$ of particles. Once they have this, from which they get a plethora of fundamental results (those listed above), they then turn to the open system by getting the time-dependent density matrix from a weighted average of the $N$-results:

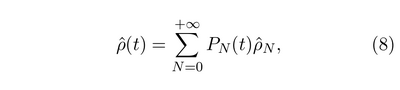
Because of the normalizations, quantities like $g^{(1)}$ or $g^{(2)}$ aren't simple weighted averages over the probabilities to be in a given $\rho_N$. This has the effect of decoupling population buildup from coherence buildup:

Therefore, the coherence of the condensate is determined not only by $\langle N\rangle$ and $T$, but also strongly depends on the particular distribution of the $P_N$.

In fact, they find that the condensation is essentially a two-mode problem. Defining $\kappa_1$ as the total pumping of all excited states:

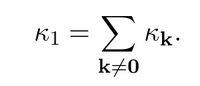
they arrive at those interesting results but those generality is unclear:

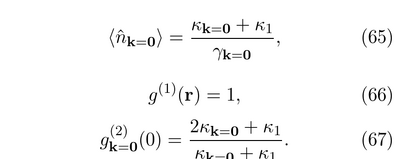
Some details of the derivations

Their dissipative-coupling relaxation:

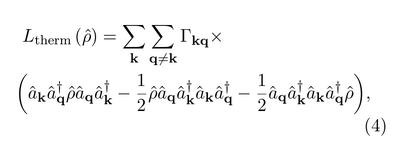
They invoke some Kubo–Martin–Schwinger relation there, which to me looks more like detailed balance.

They find that pumping the condensate destroys its coherence, although it increases its population. They also show that the linewidth of the condensate does not obey Schawlow-Townes relation in 2D.

They put pump in the decay term too, while I usually keep these completely independent. This is, however, to have a population-independent (no final-state stimulation) incoherent pumping:

which justifies it nicely enough... Maybe it's a better practice. Should revisit my old papers (say on strong-coupling) with this "understanding" of pumping.

They consider a quadratic (not polaritonic) dispersion (see end of paragraph after Eq. (15)).

Their partitions functions are analytical, although they recommend computing them through a recursive formula.

The physical meaning of G2D and G3D is the number of states in the energy range T above k = 0