Long-range ballistic motion and coherent flow of long-lifetime polaritons. M. Steger, G. Liu, B. Nelsen, C. Gautham, D. W. Snoke, R. Balili, L. Pfeiffer and K. West in Phys. Rev. B 88:235314 (2013). What the paper says!?

This page is among our 'okay articles'. It should be further expanded but we hope that it will still be useful in its present stage.

This studies polariton propagation in ultra high-Q samples:
the number of layers in both the front and back DBRs were doubled, effectively increasing the designed Q factor by more than two orders of magnitude and the designed photon lifetime from 2 to 400 ps
This is done for photon-like polaritons:
we chose a location on the wafer where the LP was mostly photonic, allowing long-distance transport.
and in a sample with a spatial potential «due to the wedge in the wafer thickness»:
In typical GaAs and other semiconductor wafers grown with molecular beam epitaxy, the thickness of the layers varies across the wafer.
So that:
This spatial gradient of the ground-state energy is the same as a force on the polaritons, since F = −∇U.
Propagation is thus also as function of the polaritonic quantum state:
On the excitonic side, the interactions are stronger, and the mass is heavier leading to greater thermalization18,19 but shorter distances for transport of the polaritons. On the photonic side, the interactions are smaller, allowing less thermalization, but much longer transport distances.
Two regimes are investigated: low (gas) & high (condensates) excitations.
The analysis is done in detail (and could be studied more by myself).
I find interesting their time of flight analysis:
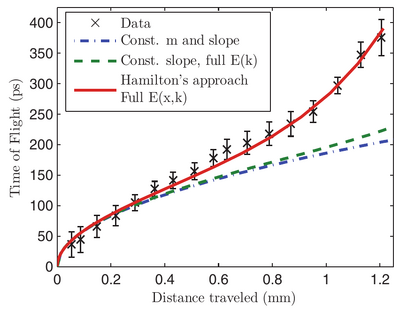
although the exact difference between the green and red is not entirely clear. In red, they seem to take into account the polariton dispersion for the mass, but not the energy, while the red also take into account the energy. It is poorly explained; their model (full Hamilton) is also interesting but they don't give details, only the Hamilton equations, not the space-dependent Hamiltonian $H(x,k)$ itself, although it probably would have not cost them much, and could be reproduced.
On propagation, this unclear comment:
It has been observed that a small excitation region can give rise to a condensate at finite k.26 It is typically the case that polariton condensates form in regions where there is substantial renormalization, since the high carrier density that allows the condensate to form also causes a real blueshift of the polariton. Therefore, it is not surprising that a condensate of small size which is formed on top of a hill will flow outward.
They also provide their own variation of the GPE to describe a self-trapping mechanism:

A big part of the paper is on the measure of the (long) polariton lifetime. There's a long discussion on how problematic it is to measure the lifetime (Sec. IV) and then details on two methods to extract it.