Quantum computing with exciton-polariton condensates. S. Ghosh and T. C. H. Liew in npj Quantum Inf. 6:16 (2020).  What the paper says!?

This page is among our 'okay articles'. It should be further expanded but we hope that it will still be useful in its present stage.

This is a theoretical proposal to implement quantum gates on qubits defined from quantum fluctuations on top of a condensate.

Even though a polariton condensate is composed of many particles, we show that number fluctuations on top of the mean-field value themselves correspond to an anharmonic oscillator in the presence of moderate polariton–polariton interactions.

This run-on sentence is unclear:

As outlined in Fig. 1, single qubit gates are controllable by laser parameters and the availability of quantum tunneling between neighboring micropillars, it is possible to realize SWAP and square-root-SWAP (sSWAP) gates, which allow for moving qubits between different pillars and universal quantum operations to establish a complete scalable quantum circuit architecture

Not only the grammar but also the intended meaning is unclear.

The model is the anharmonic oscillator:

and the condensate is a coherent state:

We define a condensate as a coherent state

Control is through short coherent pulses:

Then there is this change of variables (not entirely clear to me):

which brings them to this approximate Hamiltonian for the fluctuations:

or, in the Fock space (for fluctuations?):

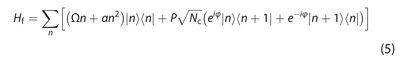
This is compared to superconducting qubits (comments after Eq. (5)).

This opening statement overlooks opposite declarations such as those of, e.g., Khitrova et al.